Johannes Kepler, Harmonices Mundi, Book II
The triangle extension theorem shows that rhombs provide a solution to the issue raised by Kepler that is quoted above. If rhombs are allowed, any vertex figure of three polygons that includes two regular polygons, one of which is a triangle, can be extended to a periodic tiling of the plane.
Proof of the triangle extension theorem
There are three cases to consider here:
a. The third polygon is a regular polygon.
Then we know from the classification of vertex types that the possible vertex figures are 3.7.42, 3.8.24, 3.9.18, 3.10.15 and 3.12.12. All of these are extendable to periodic tilings of the plane. 3.12.12 can be extended to the 3.12.12 semiregular tiling that uses only triangles and dodecagons. As for the others, there are periodic tilings already provided on this site that include these figures:
- 3.7.42 Mirror is completed using elements of SRI(3*7)
- 3.8.24 Milkmaid is completed using elements of SRI(3*8)
- 3.9.18 Warrior is completed using elements of SRI(3*9) (in fact SRI(9), which is a subset of SRI(3*9))
- 3.10.15 Nutshell is completed using elements of SRI(3*10) (in fact SRI(15), which is a subset of SRI(3*10))
b. The third polygon is a rhomb and n is odd.
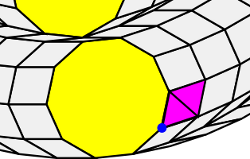
Then if α is the angle of the rhomb::
(n-2)π/n+π/3 + α = 2π
and so:
α = (2n+6)π/3n
Here we can use a simple trick.
Consider the vertex figure composed of the n-gon and the members of SRI(3n) with angles nπ/3n and (2n+6)π/3n. (You can prove to yourself that this is a vertex figures by showing that the angles add to 2π.)
By the regular polygon extension theorem proved in the previous section this vertex figure can be extended to a periodic tiling of the plane.
However the rhomb with angle nπ/3n =π/3 is the rhomb consisting of two triangles glued together.
Replace this rhomb with two triangles and we have a new vertex figure consisting of a n-gon, a triangle and a rhomb which can also be extended to a periodic tiling of the plane.
c. The third polygon is a rhomb and n is even.
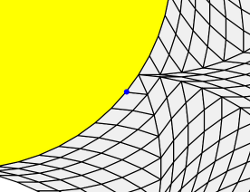
Let's use the same trick as in case b.
We have the n-gon and the rhombs with angles nπ/3n and (2n+6)π/3n.
If the rhombs are not elements of SRI(n/2) then we can then replace the nπ/3n rhomb with two triangles as in case b. and we are done.
But suppose these rhombs are members of SRI(n/2)?
We cannot apply the regular polygon extension theorem, but we can use another observation to complete the proof.
Let n = 2m. Then (2n+6)π/3n = (4m+6)π/3m = ((4/3)m+2)π/m.
Clearly this is only a member of SRI(m) = SRI(n/2) if m is divisible by 3. This means that n must also be divisible by 3 and since it is even, it is in fact divisible by 6. Let n = 6r.
Now we can use the fact that a regular polygon with 6r sides tiles the plane with a rhombic star. As you can see from the accompanying illustration, this tiling includes a vertex figure composed of a triangle, the 6r-gon and a rhomb! The rhombic star is constructed from the rhombs SRI(3r) = SRI(n/2) which is a small subset of the rhombs SRI(3n).
So the theorem is true in all three cases and we are done.
Is it possible to generalise the triangle extension theorem to include vertex figures that include any two regular polygons? Perhaps, but in order to do so we need some more machinery as we will see in the next section.
