A shape is said to have rotational symmetry if it can be mapped onto itself through rotation about a central point by some angle less than 2π. If the rotation angle is 2π/n, then the shape is said to have n-fold symmetry. All regular polygons have rotational symmetry. In fact, an n-sided regular polygon has n-fold symmetry. For example, a regular pentagon has 5-fold rotational symmetry and can be mapped upon itself through rotation by an angle of 2π/5.
As has been shown in a previous section, there are only three regular polygons that can tile the plane by themselves: the triangle, the square and the hexagon. It is of great significance that these shapes have, respectively, 3-fold, 4-fold and 6-fold symmetry. In addition, any specific rhomb (which have 2-fold symmetry) can tile the plane by itself.
There is a well known mathematical theorem called the crystallographic restriction that shows that any single shape with rotational symmetry that tiles the plane must have 2-fold, 3-fold, 4-fold or 6-fold symmetry. (Many shapes with no rotational symmetry tile the plane. There are at least 14 different irregular pentagons that do so, for example.)
The theorem is called the crystallographic restriction because the fact was first observed in actual crystals, providing an interesting example of physics and chemistry influencing pure mathematics rather than the other way round!
In 1982, Danzer, Grünbaum and Shephard pointed out in Can all tiles of a tiling have five-fold symmetry? that the crystallographic restriction only applies to tilings with a single prototile (one shape). Having said that, given reasonable restrictions (for example, a finite number of prototiles with a finite size), no tilings have been discovered in which all the tiles have a 5-fold symmetry (or for that matter, an n-fold symmetry where n is not 2,3,4 or 6). On the other hand, no one has proved that such tilings are impossible either, raising the tantalising possibility of minor mathematical renown for someone who finds such a tiling or proves that they are impossible.
The n-fold problem is described in more detail in Craig Kaplan's interesting article The trouble with five.
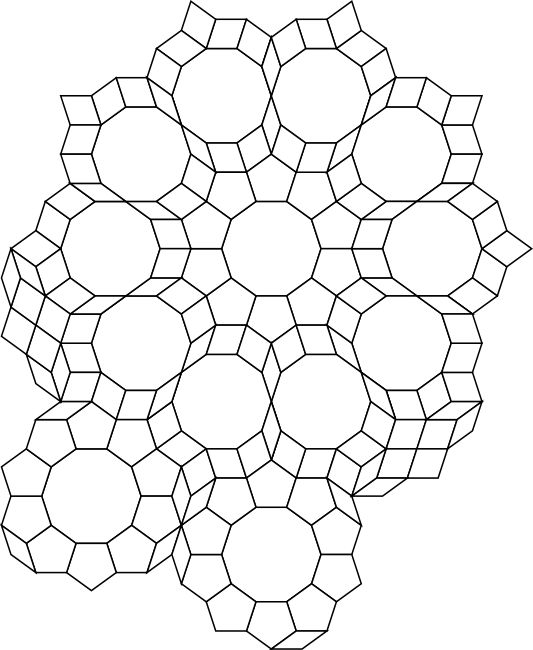
The "forbidden" vertex types described on this site give rise to many beautiful shapes with n-fold symmetry. For example, the beautiful "Extended rose" 5.5.10 tiling shown below consists mostly (but not entirely) of 5.5.10 roses with 10-fold symmetry, some with an extended 10-fold halo. These shapes need a bit of help from small rhomb patches with 2-fold symmetry however to tile the plane. This is best seen in the alternative colouring version.
The next few chapters of this site look at tilings extended from the 5.5.10, 4.5.20 and 3.10.15 vertex figures that include shapes with 5-fold or 10-fold symmetry. None of these shapes tile the plane by themselves but who knows, perhaps some combination of them might do the trick?
One interesting starting point might be this infinite strip of interlocking 5.5.10 roses composed of pentagons and decagons.
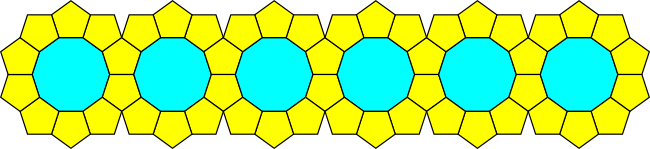
Since decagons have 10-fold symmetry, they automatically have 5-fold symmetry as well. Can you find a similar strip also composed of 5-fold shapes that interlocks with the rose strip so that the two tile the plane together? Or alternatively, can you prove that such a strip is impossible?
Warning: looking for n-fold tilings can be addictive!
Extended rose - a 5.5.10 tiling

Translational unit
Legend

Skeleton tiling
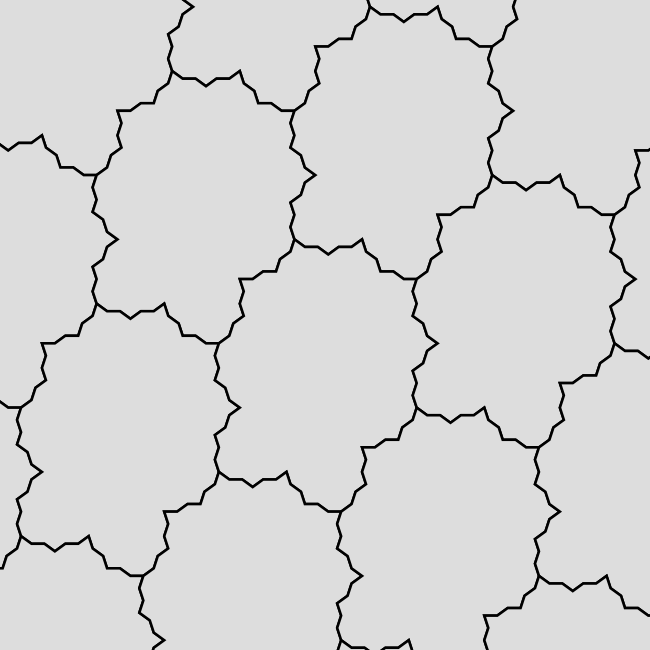
Tiling (alternative colouring)

Translational unit (alternative colouring)
Tiling (black and white)