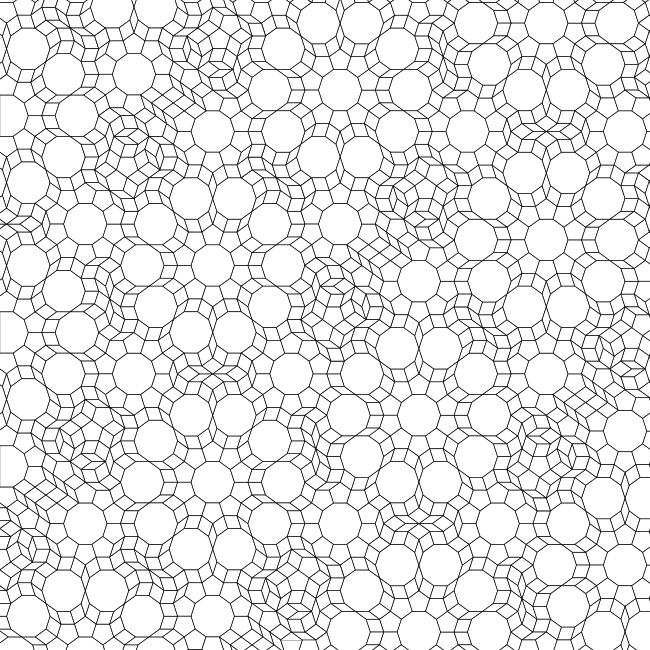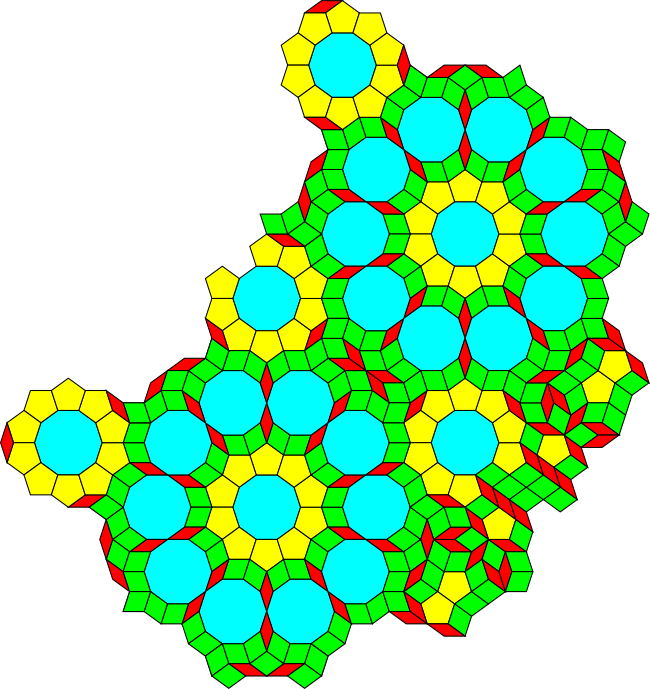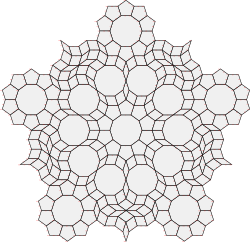
In this and the following section, I'll provide a Dürer construction for thick and thin tilings for the more elaborate five-fold tile patch to the right. As it turns out, the resulting thick and thin patches have a very interesting property that will be described in the chapter on Penrose substitution.
We can arrange this patch in the same pattern as Dürer's thin tiling if we allow some overlap as we can see in the image below. Vertically it is possible to overlap two of the 5-fold patches so that the polygons match exactly. Horizontally, however, there is an inconsistency. Different tile shapes overlap. In order to extend this to a tiling, we will need to delete some of the polygons in the rhomb-shaped gap and fill this gap with a consistent pattern.
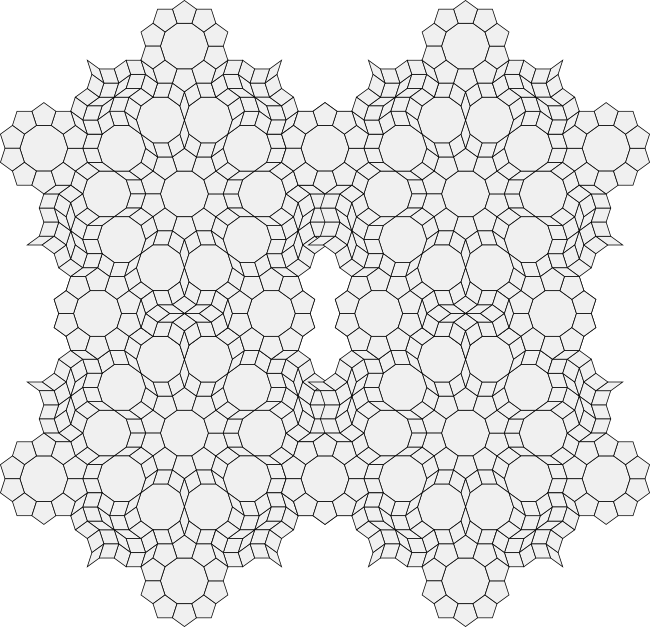
It turns out that this can be done as can be seen in the tiling below. There is something slightly strange to my eye about the pattern of tiles in the rhomb-shaped gap. I think of this as a "broken rose" tiling. Despite a number of attempts, I have not succeeded in filling the gap without breaking the roses.
Those with sharp eyes will notice that the gap also features two patches of rhombs that form fused decagons - perhaps relatives of the ones that appear in Kepler's Aa tiling?

Translational unit
Legend

Skeleton tiling
Tiling (black and white)