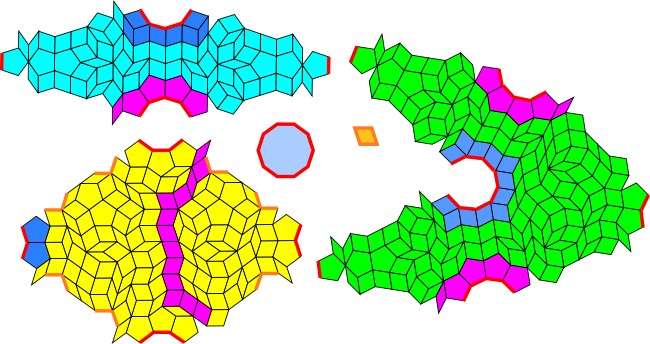
What is surprising about the thin and thick patches in the tilings described in the last two sections is that with some small modifications they can be made to act like the thin and thick rhombs themselves. In particular, they can be used to construct something like Penrose tilings.
Roger Penrose discovered this class of tilings in the 1970s when investigating the aperiodic prototile set problem. The problem was to construct a set of prototiles that can tile the plane but never create a periodic tiling. It was once thought that this was impossible, but then in 1964, Roger Berger published a (very large) set of such prototiles in his doctoral thesis. Subsequent work by others reduced this to a set of 92 prototiles.
Roger Penrose reduced this still further and found three sets of aperiodic tiles with 4, 2 and 2 members respectively. The third of these sets, called P3, consists of the thin and thick rhombs (10-rhomb and 5-rhomb). Obviously these rhombs can tile the plane periodically, but Penrose added adjacency conditions which specified how the rhombs were allowed to combine. These conditions prevent the rhombs from creating periodic tilings.
The conditions can easily be shown visually, either through colour patterns or making small notches in the rhombs:
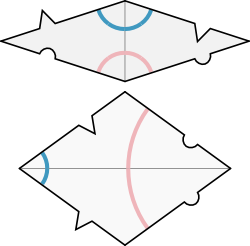
The rhombs can only combine if the notches fit together and if the blue circle and maroon curve is not interrupted. The notches and colour patterns are two different ways of specifying the same adjacency conditions. So only one of these needs to be used in practice. Usually the colour patterns are used because they can be left on the full tiling and make it more decorative.
Here is a larger tiling patch based on these adjacency conditions:

Penrose tilings are quasiperiodic, which means that any specific patch is repeated infinitely often even though the tiling is not periodic. These tilings have attracted a lot of interest from both recreational and professional mathematicians because of their aesthetic appeal and unusual fivefold local symmetry.
It is possible with a bit of effort to construct an aperiodic tiling set from the thin and thick tiling patches described in the last two sections.
Here are the modified patches themselves marked with a similar Penrose colouring pattern:
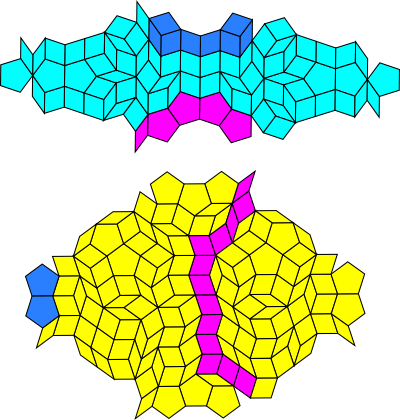
The thick patch can combine with itself and with the thin patch and in this way acts exactly like the thick rhomb. Like the thick rhomb, five copies of the thick patch can be arranged in a circle around a central point (with a decagon hole at the centre!).
There are a couple of complications, however. Fortunately they can both be solved.
First, the thin patch cannot combine with itself. As it happens, the Penrose adjacency conditions allow the thin rhomb to combine with itself in only one way, and we can introduce a third patch to cover this condition:

This third patch looks like a nutcracker to me.
We can then define a simple substitution that converts any Penrose rhomb tiling into one using these patches:
- replace any two adjacent thin rhombs with the green nutcracker patch,
- replace all other thin rhombs with the blue thin patch, and
- replace all thick rhombs with the yellow thick patch,
making sure that the colouring pattern is maintained.
As an example, here's a small patch from a Penrose rhomb tiling:

and the resulting substitution tiling:
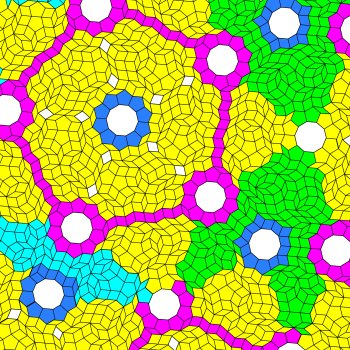
This last image reveals the other difficulty: the substitution tiling has decagon and 5-rhomb shaped gaps. In fact, there is a decagon-shaped hole for every vertex of the original tiling and at least one and usually two rhomb gaps whenever two yellow patches are adjacent.
Fortunately, this is easily fixed by adding these shapes to the prototile set with appropriate adjacency rules.
Here then is the full set of five aperiodic patches with the adjacency colours:
The image is linked to an SVG file. (You will need to download it and open it in Inkscape or some other SVG editor to view it.)
The adjacency rules are as follows:
- The dark blue circle and maroon paths must be unbroken.
- The decagon can only be adjacent to red edges.
- The 5-rhomb (thick rhomb) can only be adjacent to orange edges.
- The orange and red edges are ignored when positioning the blue, yellow and green patches.
Notice that it is OK if maroon and non-maroon pentagons both touch the same decagon - the dark blue tiles always surround a decagon but the maroon tiles can follow a more irregular path so long as they continue.
I have set up the blue, yellow and green patches so that they should never be able to fit together geometrically in violation of the blue and maroon adjacency rules (the tiles just won't fit). So in this case the colour rules are likely redundant. But actually proving that looks tough. With the colour rules it is clear since the five patches then mimic the same adjacency rules as the Penrose rhombs.
It is curious that these patches can be made to act like the Penrose rhombs. This is certainly not true of all thick and thin patches that can be derived through the Dürer construction. But there may be others with this property. The next chapter describes a construction of a thin tiling from a 5-fold patch extended from the 4.5.20 vertex figure that seems promising and has other interesting properties.