
The great Renaissance artist Albrecht Dürer published his treatise Underweysung der Messung mit dem Zirckel und Richtscheyt (A Course in the Art of Measurement with Compass and Ruler, often simply called the Painter's Manual) in 1525, almost a century before Harmonices Mundi. The Painter's Manual summarised a life time of experience as one of the leading painters and engravers of the early Renaissance. Dürer died three years after it was published.
Google has placed an English translation of the Painter's Manual online, but unfortunately, unlike their online translation of Harmonices Mundi, it has restricted access and it is only possible to search for small text fragments.
The original text is available here if you can read German gothic script or simply want to appreciate the beautiful layout and design of the book. Dürer was a leading advocate of good typography and dedicated a section of the Painter's Manual to discussing the best techniques. If you are going to publish a technical document, it is a major advantage to be an artistic genius!
Another option is the Wikisource version here which has been transliterated into a modern character set. Unfortunately Google Translate does not appear to be able to make much of Dürer's dialect. The best option if you are not a German speaker and want to read the whole treatise in translation is probably to try to track it down in an academic library.
Regular polygons

Like Kepler, Dürer was fascinated with regular polygons and polyhedra, although more for their practical visual possibilities than as the basis for mathematical theories.
A large section of the Painter's Manual is dedicated to practical ways to construct various curves and regular polygons with a ruler and compass. Kepler goes over some of the same ground in the first book of Harmonices Mundi but only includes mathematically exact constructions. The more pragmatic Dürer also includes approximations, including one for the regular heptagon. (It can be proven that there is no exact construction using ruler and compass for this shape.)
Dürer was one of the first people to provide flat paper models that can be folded into polyhedra and provides more than a dozen examples.
The Painter's Manual also include a brief section on polygon tilings. Dürer illustrates the three regular tilings consisting respectively of squares, triangles and hexagons, as well as the 4.8.8 octagon tiling and the 3.6.3.6 uniform tiling with its striking six pointed star pattern. He also shows examples of non-edge-to-edge tilings with triangles and squares. According to the introduction to the English translation, Dürer's tiling illustrations may have been inspired by flooring patterns he observed on a trip to the Netherlands.
Rhomb tilings

Three rhomb tiling examples from the Painter's Manual.
Perhaps the most interesting part of the tiling section of the Painter's Manual, however, is Dürer's examples of rhomb tilings. A rhomb (or more traditionally rhombus) is the simplest geometric shape beyond the regular polygon. Like a regular polygon, all the edges of a rhomb have the same length. However, a rhomb can have two different angles instead of one. All rhombs have four sides and in this sense they can be considered generalisations of squares. Indeed, a square can be defined as a rhomb with both angles equal.
If one angle of a rhomb is α, then the other is always π-α, so given a fixed edge length and orientation, a rhomb can be uniquely defined by specifying one angle. In this way they also resemble regular polygons, which can also be uniquely defined by specifying a single angle.
Like a square, any rhomb can tile the plane by itself and Dürer gives an example of such a tiling in the Painter's Manual. (This is the third illustration in the image above.)
There are other interesting tilings of the plane that also work for any rhomb regardless of angle. One (not given by Dürer) is illustrated below. It uses rhomb, hexagon and triangle prototiles. You can see that the same pattern works regardless of the rhomb used and the same vertex type occurs everywhere so we might call this a uniform tiling using both rhombs and regular polygons. (Note that when the rhomb is a square, this becomes the 3.4.6.4 semiregular tiling.)

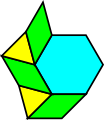


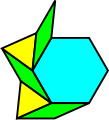

This pattern works because each vertex always includes both the small angle and the large angle of the rhomb, so if the rhomb angle is α then the sum of the angles is α + (π - α) = π. The sum is therefore always π and does not depend upon the rhomb used.

Dürer also includes examples of tilings that depend upon specific rhombs. The middle example from the three tiling examples from the Painter's Manual shown above is sometimes called the Necker cube because it creates an illusion of three dimensional cubes. The small angle of the rhomb he uses is π/3.
Kepler also includes a Necker cube rhomb tiling in Harmonices Mundi, illustrated in his diagram G.
The n-rhombs and fractional rhombs
The first example from the Painter's Manual above shows that a certain class of rhombs can form a complete vertex star. In this example 8 identical rhombs meet at a central point. In general, a rhomb which allows n copies to meet at a single point has small angle 2π/n.
There seems to be no common name for rhombs with this property. On this site, I will call a rhomb with the angle 2π/n an n-rhomb.
If a rhomb's small angle does not divide evenly into 2π, I will call it a fractional rhomb.
There is a very close connection between an n-rhomb and an n-sided regular polygon. This is because the larger angle of an n-rhomb is π - (2π/n) = (n-2)π/n, which is the formula for the interior angle of an n-sided polygon.
In a sense, n-rhombs are fragments of n-sided polygons and the larger angle of an n-rhomb can replace an n-sided regular polygon in any vertex figure involving that polygon. This fact is important for many of the rhomb tilings we consider on this site.
Other tilings
Dürer includes a number of other unusual tilings in the Painter's Manual including one with rhombs and hexagons, a tiling with octagons and irregular triangles, and even several tilings with heptagons and kite-like shapes.
In the next section I'll give special attention to Dürer's tilings involving rhombs and pentagons.
