William Shakespeare, Hamlet, Act II, Scene II
As Kepler proved in Harmonices Mundi, the 3.10.15 vertex figure can never be part of a rose, because a triangle and a decagon cannot alternate around the odd-sided 15-gon.
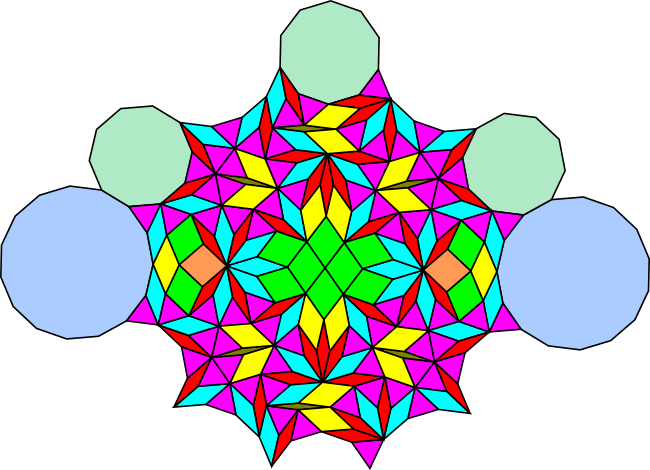
However, this 3.10.15 tiling contains something much stranger - a nutshell. A nutshell is a bit like the reverse of a rose. Whereas a rose is a ring of smaller polygons around a larger polygon, a nutshell is a ring of larger polygons enclosing a patch of smaller ones. In this case the vertices of the larger polygons (the decagon and the 15-gon) do not all have the same type, so perhaps we could call this an imperfect nutshell.
In this tiling, the larger polygons form a hexagonal honeycomb that extends indefinitely and the smaller tiles sit inside the hexagonal cells. The polygon patches inside each cell can be rotated individually so we can use this basic pattern to construct an uncountable number of nutshell tilings.
It is easy to see that a pair of regular polygon prototiles can form a hexagonal ring if one has an even number of sides, and the other has a number of sides divisible by three. This is not only true for the larger polygons of the 3.10.15 figure, but also for the 3.8.24 and the 3.9.18 figures. It would be interesting to know if these also have nutshell tilings.
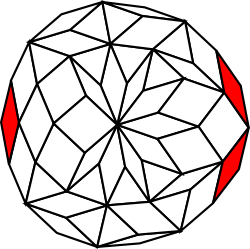
This tiling contains two copies of a large mysterious jewel like patch of polygons. This can be best seen in the black and white version of the tiling and is a convex irregular polygon with three 15-rhomb chunks removed from it. I've added back the missing rhombs in the illustration. Such beautiful structures often occur in these rhomb tilings.
The tiling requires 9 prototiles to complete: 3 regular polygons, 4 n-rhombs and two fractional rhombs. As I note in the polygon legend below, all six rhomb prototiles have small angles that are multiples of π/15.
(As defined in the Painter's Manual section of this site, a fractional rhomb is one whose small angle does not divide evenly into 2π and so repeated copies cannot form a vertex figure.)
I have not been able to find a way to extend the 3.10.15 or 3.7.42 vertex figures without using fractional rhombs. In this sense it appears that these figures are more "imperfect" than the other "forbidden" figures. This is still a conjecture, however. I have not proved yet that tilings without fractional rhombs are impossible for these figures.
The prototile set used for this tiling is a maximal set in the sense that it contains all possible rhombs with angles that are a multiple of π/15 with the exception of 5π/15. This last rhomb is just two triangles glued together, however, so the triangle can easily substitute. As a result, any incomplete vertex star with a single gap (two polygons without two adjacent edges) constructible with these prototiles can always be completed using these prototiles.
You can read this chapter to find out more about this remarkable prototile set and another interesting nutshell tiling.
There is something intriguing about the fact that one of the prototiles needed to complete this tiling is the 30-rhomb. The larger angle of this rhomb acts like a 30 sided regular polygon. The 3.10.15 figure is unique among all the "forbidden" vertex figures because the number of sides of the largest polygon is not a multiple of the number of sides of the second largest polygon. Based upon the example of the other "forbidden" figures, one would have expected this figure to actually be 3.10.30 and it may be significant that a 30-rhomb is needed to complete the tiling.
Tiling

Translational Unit
Legend

Skeleton tiling

Tiling (Black and white)

Translational Unit (Black and white)