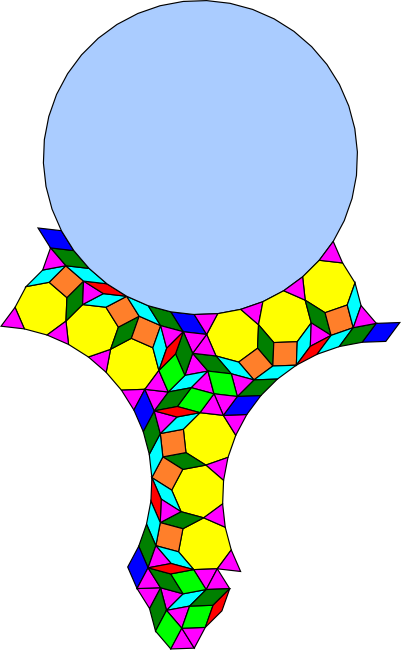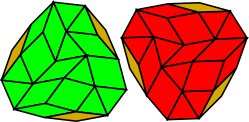
The translational unit for this tiling looks like an occult hand mirror to me. This is especially obvious in the alternative colouring below.
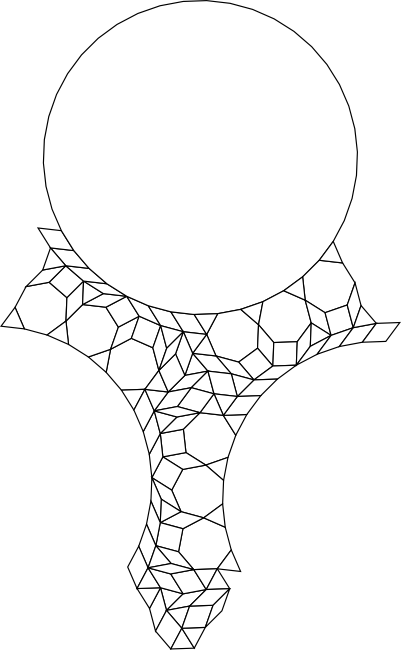
Like the 3.10.15 Nutshell tiling, this tiling requires nine prototiles to complete. In this case these are three regular polygons, one 14-rhomb and five fractional rhombs. As shown in the legend, the small angles of all the rhomb prototiles are multiples of π/21.
(As defined in the Painter's Manual section of this site, a fractional rhomb is one whose small angle does not divide evenly into 2π and so repeated copies cannot form a vertex figure.)
I have not been able to find a way to extend the 3.10.15 or 3.7.42 vertex figures without using fractional rhombs. In this sense it appears that these figures are more "imperfect" than the other "forbidden" figures. This is still a conjecture, however. I have not proved yet that tilings without fractional rhombs are impossible for these figures.
Although it is possible to construct a rose with 3.7.42 vertex figures, curiously, this tiling does not contain a full rose. Instead it contains a strange partial rose in which a sequence of three heptagons is followed by a sequence of rhombs. The partial roses are formed in such a way that the heptagon portions and rhomb portions can join together in adjacent translational units. It would be interesting to know if a 3.7.42 tiling is possible with a full rose of alternating triangles and heptagons centred on each 42-gon.
This tiling also contains a prominent jewel like patch of polygons, best seen in the alternative colouring tiling. It is an irregular convex polygon with three 21-rhomb shaped chunks removed. I have shown this in the accompanying illustration which adds back in the missing 21-rhombs. (Note that the 21-rhomb does not occur in the tiling itself.) The jewel occurs in right and left handed forms. There is no way to transform the right handed form into the left handed form using translations or rotations - a mirror reflection is needed.
Tiling

Translational Unit
Legend

Skeleton tiling

Tiling (Alternative colouring)

Translational Unit (Alternative colouring)
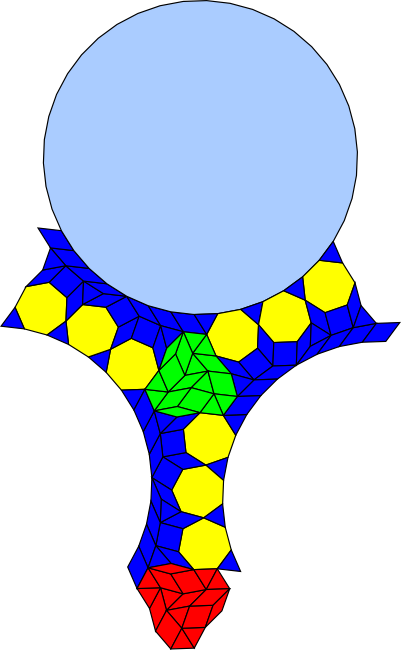
Tiling (black and white)
Translational Unit (black and white)