Albrecht Dürer, Book 2, The Painter's Manual, 1525

Dürer illustrates four pentagon tilings in the Painter's Manual. Two of these are periodic tilings. The first and simplest combines pentagon and 10-rhomb prototiles and could perhaps be called the "thin" tiling.
The second tiling also contains pentagon and 10-rhomb prototiles but changes the tiling pattern to add gaps that can be filled by 5-rhombs. We could call this the "thick" tiling because of the thicker appearance of the 5-rhomb. The 5-rhomb and 10-rhomb play an important role in the modern theory of Penrose tilings, where they are often informally called the thick and thin rhombs.
You can view the thick tiling at the bottom right of this Wikisource page.
Dürer's third tiling contains a unique central pentagon and so cannot be periodic. In his interesting article on pentagon tilings, The trouble with five, Craig Kaplan points out a variant of this third tiling with a central rose (a decagon surrounded by pentagons) that is continued by a spiral pattern of pentagons and 10-rhombs.
Dürer does not show how to complete his fourth tiling, which also has a central pentagon, but merely remarks that the "leftover areas you can then fill with whatever you like". It is possible that these empty spaces could be filled with rhombs but without more information it is unclear what Dürer had in mind.
You can view Dürer's third and fourth tilings on Wikisource.
Kepler's Aa

Kepler knew that pentagons could not occur in edge-to-edge plane tilings of regular polygons. In Harmonices Mundi he also discussed the fact that pentagons can appear in tilings of the sphere, where they form the basis of the dodecahedron.
Like Dürer, Kepler could not resist looking beyond regular polygons to see if he could find plane tilings involving pentagons. His solution, which he illustrated as diagram Aa in Harmonices Mundi, involved five pointed stars and a peculiar fused double decagon shape. The tiling was more complex than any of Dürer's and Kepler himself noted that the "structure is very elaborate and intricate".
Craig Kaplan points out in The trouble with five that several mathematicians have proved that Kepler was correct and that his Aa diagram can be continued into a tiling of the plane. Kaplan says that Kepler called his fused double decagon shapes "monsters" but does not say where the term comes from. It does not appear in Harmonices Mundi, where Kepler described the shape much more prosaically as a "combined decagon".
A 5.5.10 rhomb tiling
Kepler's Aa tiling contains vertices with type 5.5.10 and indeed an entire 5.5.10 rose with a decagon surrounded by a ring of pentagons. But it also includes other complex shapes such as five-pointed stars and combined decagons. Is it possible to extend a 5.5.10 vertex figure to a full tiling using the simpler 5-rhomb and 10-rhomb shapes from Dürer?
Indeed it is, as the following example shows.
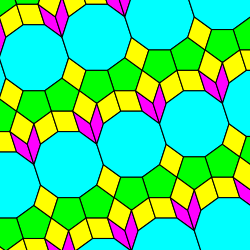
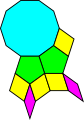

This is the simplest periodic tiling that I could find that includes a vertex with the 5.5.10 type. More complex 5.5.10 tilings are also possible using 5-rhomb and 10-rhomb prototiles and we will look at some elsewhere in the site.
