The standard Dürer construction technique does not seem to work very well for tilings extended from the 3.10.15 vertex figure, or at least I have not been able to construct any using that technique.
Nevertheless, it is possible to construct a 3.10.15 tiling with some local five fold symmetry using nutshells. The result is an interesting complement to the hexagonal Nutshell tiling provided above.
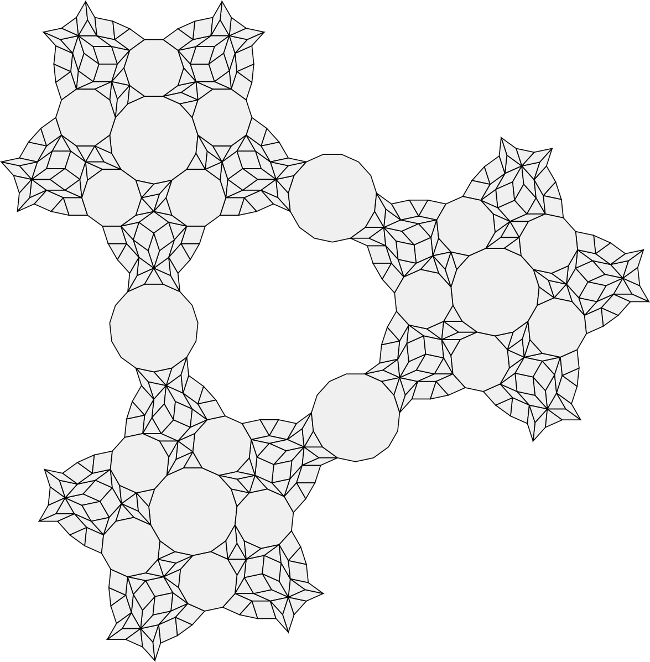
There are at least four nutshells constructible using the prototiles from the Nutshell tiling. In the first of these, the inner patch of smaller polygons intersects with two edges of each larger polygon in the outer ring. In the second nutshell, the inner patch intersects with three edges of each of the outer polygons. In the third hexagonal nutshell, the intersection is with four edges of each of the outer polygons. Finally, a fourth irregular nutshell is possible.

The patch of smaller polygons in the hexagonal nutshell appears complex, but as you can see from the alternative colouring at the lower right below, most of it is made up of four copies of the patch from the second nutshell! The rest of the tile patch inside the hexagonal nutshell is made up of two copies each of four other shapes.
The hexagonal nutshell is the basis of the Nutshell tiling described before. The other three nutshells can be combined to form another interesting tiling with some five fold local symmetry. I call this tiling "Mixed nuts" for obvious reasons.
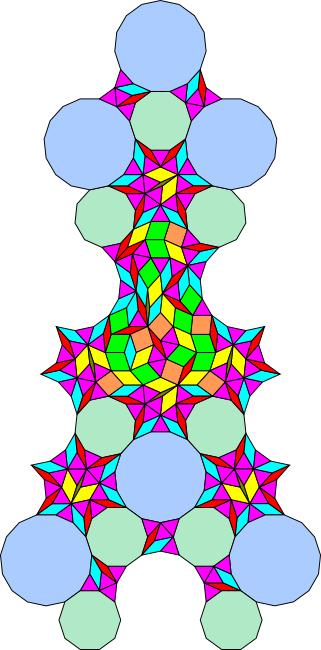
Tiling

Translational Unit
Legend

Skeleton tiling

Tiling (Black and white)

Translational Unit (Black and white)
More on the Nutshell prototiles
Many beautiful shapes can be constructed with the Nutshell prototiles. Below are just a few examples.
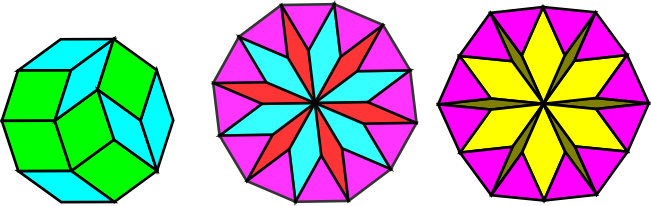
The 5-rhomb and 10-rhomb combine to form a decagon, showing that the decagon is in a sense redundant in this prototile set. This is a consequence of a well known theorem showing that every regular polygon with an even number of sides can be decomposed into rhombs.
Perhaps more surprisingly, the 10-rhomb, 15-rhomb and triangle combine to form a regular dodecagon. Because it is a regular dodecagon, it tiles the plane along with a triangle following the pattern of the 3.12.12 uniform tiling. Moreover, the 30-rhomb combines with the fractional 4π/15 rhomb and a triangle to form an irregular dodecagon. Despite its irregularity, this shape also tiles the plane with a triangle!
It is also possible to construct interesting pentagonal shapes with this prototile set as the image below shows. These shapes can combine with the 15-gon to create larger shapes with three-fold symmetry.
I have not yet been able to figure out if it is possible to extend a pentagonal patch constructed using these prototiles to a full periodic tiling of the plane. If several patches with five-fold symmetry can be combined to tile the plane, this would answer an important open question in tiling theory, as described in Craig Kaplan's interesting article The trouble with five.