In the Painter's Manual, Dürer gives four examples of pentagon tilings. Two of these are periodic. The first of these, the thin tiling, combines the 10-rhomb (often called the thin rhomb) with pentagons as described in the section on pentagon tilings. The second of these, the thick tiling, rearranges the thin tiling to create additional 5-rhomb (thick rhomb) gaps.
Dürer's constructed these tilings by arranging pentagons in a specific pattern and then filling in the gaps with rhombs.
It is possible to create an infinite number of shapes with pentagonal (5-fold) symmetry by extending the 5.5.10, 4.5.20 and 3.10.15 vertex figures. We know from the crystallographic restriction that none of these shapes can tile the plane by themselves. But is it possible to use Dürer's constructions to arrange some of these shapes in a specific pattern and then to fill in the gaps to create a tiling?
The answer in at least some cases is yes. The construction will not always result in a tiling as this depends upon the available prototiles.
The full construction given any tile patch α ("alpha") with 5-fold symmetry is:
- Make a copy of the shape and rotate it by π radians (180°).
- Join this to the bottom of the original shape, possibly by overlapping common polygons and filling in any gap with a buffer patch. Call this new double patch β ("beta").
- Make a copy of β and place it to the right of β . The polygons required to fill the gap between the two β patches form the thin patch. Give the name γ ("gamma") to the shape formed by the two copies of β with the thin patch between them. β together with the buffer patch and thin patch will tile the plane. This is called a thin tiling.
- Place one copy of γ below the other and fill in the gap between them. The polygons required to fill in the gap between the two γ shapes form the thick patch. We'll call this final shape δ ("delta") (two γ patches with the thick patch between them). δ contains 8 copies of the original 5-fold shape plus the buffer, thin and thick patches. The β patch together with the thin and thick patches will also tile the plane. This is called a thick tiling.
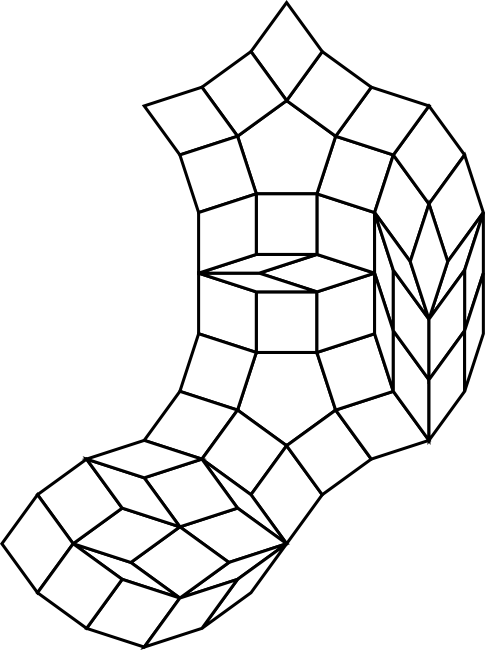
To make this clearer, here is a diagram of such a construction. The initial 5-fold shape is the centre of the globe jewel that appears in the Globe 4.5.20 tiling. The thin patch is shown in light blue and the thick patch in orange.

The full thick tiling is shown below. I was not able to construct the thin and thick patches in this case without adding the 3π/10 fractional rhomb to the prototile set used for the Globe 4.5.20 tiling.
A simple 4.5.20 thick tiling

Translational Unit
Legend

Skeleton tiling

Tiling (Black and white)

Translational Unit (Black and white)