The Penrose substitution tiling described in the previous chapter was constructed from patches made up of the same prototiles used by the Gears 5.5.10 tiling. A striking aspect of this substitution tiling is that every vertex of the original Penrose tiling is replaced by a decagon. The thick patch combined with itself and the thin patch in exactly the same way as a thick rhomb, and the thin patch acted enough like a thin rhomb to make the substitution work given the Penrose adjacency rules.
Not all thick and thin patches combine like this however. The thick and thin patches from the original Dürer construction example have some interesting symmetries but do not combine like the Penrose rhombs.
Is it possible to construct a Penrose substitution tiling from the same prototiles used by the Globe 4.5.20 tiling? If so then we might have a substitution in which every Penrose vertex becomes a 20 sided polygon (sometimes called an icosagon).
In this chapter I construct a thin patch from the 4.5.20 prototiles that has a subset that behaves exactly like the thin rhomb. In this case, the subset combines with itself and like the thin rhomb, 10 copies can be arranged around a central point (with an icosagon hole at the centre!). The thin patch and indeed the thin tiling constructed from it has a very interesting, complex and beautiful structure.
Here is the 5-fold patch that we will start with:

This patch seems complex but in fact it is constructed entirely by overlapping copies of a single 16-sided irregular polygon with copies of the 4.5.20 rose. I have no idea why this specific 16-sided irregular polygon appears so prominently. Because it does, however, I think of it as the crown jewel.
We can construct the γ patch for the tiling by reversing a copy of the five-fold shape and placing it below the original shape and then placing two copies of this double shape side by side. I've modified the standard Dürer construction by overlapping some of the roses. We now must fill in the gaps in the shapes to get the buffer and thin patches. The diagram below shows the γ patch before we've filled in the gaps:

After a bit of effort I was able to construct a buffer patch out of the same prototiles used for the 5-fold shape. This will fit below and above two of the 5-fold shapes. It has some unusual properties.
Here is the buffer patch with sections marked in green, maroon and yellow:
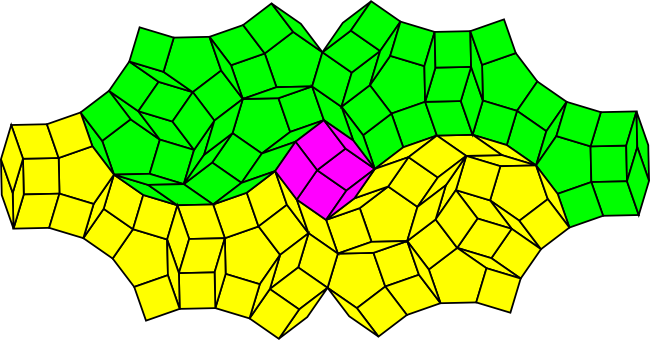
If we rotate the green patch by 180°, we can see that it is identical to the yellow patch! Moreover, the two patches look as though they are composed of the fragments of a small number of convex polygons. I admit the last comment is a bit subjective, but as you will see, the thin patch has even more of these jewel fragments or shards.
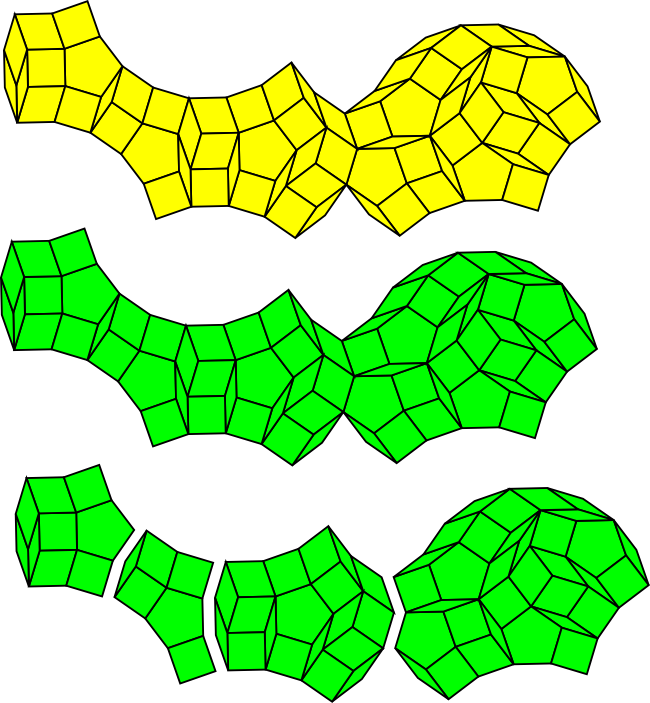
Here is the completed gamma patch - I've actually added the yellow patch above to all the sides of the 5-fold patch, which made deriving the thin patch in the centre much easier.
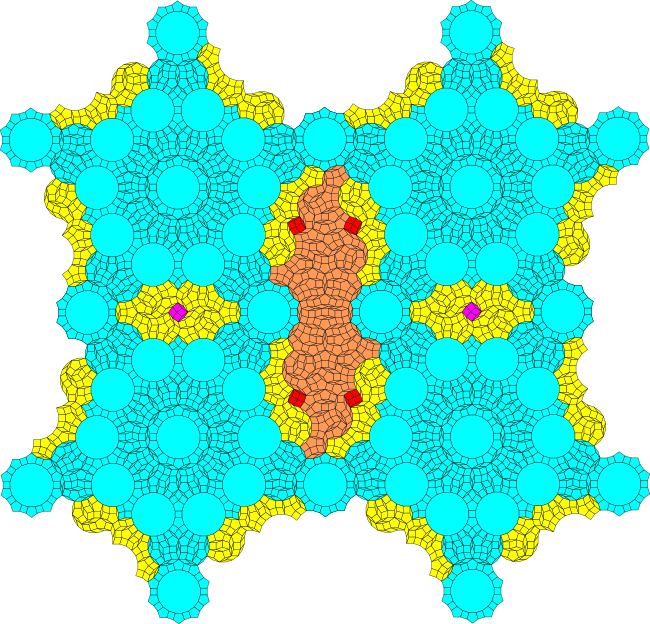
The central part in orange is the subset of the thin patch that acts like the thin rhomb. It has some interesting properties as described in More on a 4.5.20 thin rhomb patch.
There are already enough large images on this page, so you find the final thin tiling here: Jeweled crown - a thin 4.5.20 tiling.
