It is a surprising fact that 6 of the 21 possible vertex figures cannot be extended to any edge-to-edge regular polygon tiling. Since these "forbidden" vertex figures are the only ones that contain a pentagon (and a heptagon, nonagon and other larger polygons) this immediately implies that no edge-to-edge regular polygon plane tiling can contain any of these polygon types.
The vertex figures from the three families analysed before this point have prototiles chosen from a set of only 5 polygon types: the triangle, square, hexagon, octagon and dodecagon and so this result implies that only these 5 prototiles can form any edge-to-edge tiling of regular polygons.
Moreover, since the octagon occurs in only one legal vertex type, it can only occur in the unique 4.8.8 uniform tiling. So the result is actually even more restrictive and can be described in this remarkable theorem:
Prototile theorem
With the exception of the unique 4.8.8 uniform tiling, any edge-to-edge plane tiling of regular polygons must be constructed from equilateral triangle, square, regular hexagon and regular dodecagon prototiles.
This (to me at least) unexpected result is not difficult to prove using the Gap theorem mentioned before and so I will do so below.
The forbidden vertex types
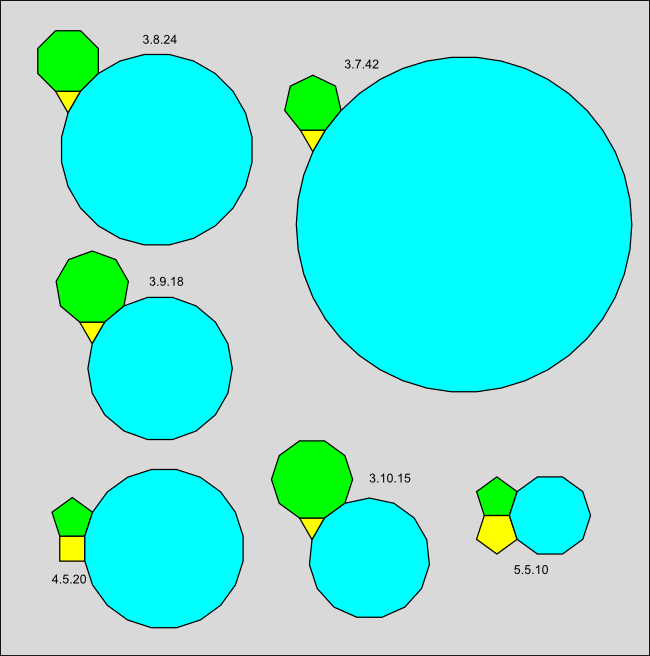
Proof of the prototile theorem
Let us start by showing that the 6 vertex figures above cannot occur in any edge-to-edge regular polygon tiling.
There are really only two cases to consider. Case 1 is the vertex types 3.7.42, 3.8.24, 3.9.18 and 3.10.15 as the same argument works for all four types. Case 2 is the vertex types 4.5.20 and 5.5.10 as the same argument works for both types.
Let us start by using the vertex type 3.10.15 as an example for Case 1 and assume for contradiction that it can be extended to a tiling of the plane by regular polygons. Start with the three polygons intersecting at the white vertex and ignore the purple 15-gon for now. If we consider the decagon and triangle intersecting at the red vertex, then the angle sum of these two polygons is (8π/10+π/3 = 34π/30). The gap angle is then 2π - 34π/30 = 26π/30.
This is less than or equal to π and so the Gap theorem applies. The gap ratio g is 26/30 and m = 2/(1-g) = 15. By the Gap theorem, the only solution is a 15 sided polygon. But if we insert this polygon (shown in purple in the diagram), it overlaps the other 15-gon, contradicting our assumption that a tiling is possible.
Exactly the same argument applies to the vertex types 3.7.42, 3.8.24, and 3.9.18 and shows that none of these types can be extended to a tiling by regular polygons. In essence, there is not enough room to fit the required large polygons.

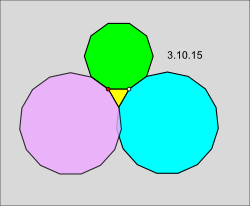
Let us start by using the vertex type 5.5.10 as an example for Case 2 and assume for contradiction that it can be extended to a tiling of the plane by regular polygons. Start with the three polygons intersecting at the white vertex and ignore the purple polygons for now. We will now add the purple polygons one by one, each the only option allowed by the Gap theorem and then as before derive a contradiction caused by an overlap.
Consider the two pentagons intersecting at the lower green vertex. The angle sum for these two pentagons is 3π/5 + 3π/5 = 6π/5. The gap angle is 2π-6π/5 = 4π/5. This is less than or equal to π so the Gap theorem applies. The gap ratio is g = 4/5 and m = 2/ (1-(4/5)) = 10. By the Gap theorem, the only possible solution is a decagon. Add this as decagon a.
Now consider decagon a and the green pentagon intersecting at the higher green vertex. The angle sum for these two polygons is 8π/10 + 3π/5 = 14π/10. The gap angle is 2π - 14π/10 = 6π/10. This is less than or equal to π so the Gap theorem applies. The gap ratio is 6/10 and m = 2/(1-(6/10)) = 5. By the Gap theorem, the only solution is a pentagon. Add this as pentagon b.
Now consider pentagon b and the green pentagon intersecting at the red vertex. As before, the angle sum for these two pentagons is 3π/5 + 3π/5 = 6π/5. The gap angle is 2π-6π/5 = 4π/5. This is less than or equal to π so the Gap theorem applies. The gap ratio is g = 4/5 and m = 2/ (1-(4/5)) = 10. By the Gap theorem, the only possible solution is a decagon. Add this as decagon c.
We can now derive our contradiction because decagon c intersects the original blue decagon in the vertex figure. This contradicts our original assumption that it is possible to extend the 5.5.10 vertex figure to a tiling of regular polygons.
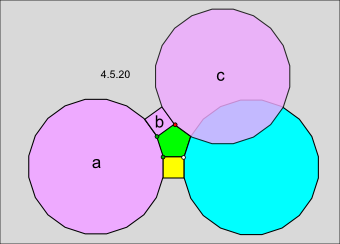
The same argument applies to the vertex figure 4.5.20 except that it involves a square and a pentagon instead of two pentagons and results in an even larger overlap between 2 20-gons.
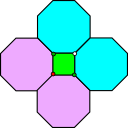
Having eliminated the 6 vertex figures in this family, we are almost finished proving the Prototile theorem. All that is left to prove the uniqueness of the 4.8.8 tiling. There are no other legal vertex types involving octagons, so it is clear that every octagon vertex in an edge-to-edge regular polygon tiling must have the 4.8.8 type, but why do all the square vertices in a tiling with octagons also have to have this type? See the 4.8.8 figure located around the white vertex in the illustration to the left. If we consider the two green vertices in the illustration, they also include octagons and so we are forced to add a second purple octagon for each green vertex in order to continue the tiling. But this completes the fourth red vertex as well, showing that octagons must be attached to every square vertex.
The other 14 legal vertex types include only triangle, square, hexagon and dodecagon prototiles and so this completes the proof.
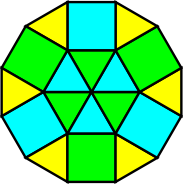
This result is still more restrictive than it seems, because as you can see from the illustration to the right, a regular hexagon can be decomposed into triangles and a regular dodecagon into triangles and squares. Thus we have this central result:
Catalog theorem
To construct a catalog of all edge-to-edge regular polygon tilings, it is necessary only to start with the 4.8.8 uniform tiling and add all possible tilings with equilateral triangle and square prototiles.
The remaining tilings can be constructed by replacing some of the hexagon shaped patches of triangles with hexagons, and replacing some of the dodecagon shaped patches of triangles and squares with dodecagons.
Brian Galebach catalogs hundreds of regular polygon tilings on his interesting website on n-uniform tilings. Many of these are quite beautiful. Nevertheless, it seems aesthetically disappointing that the range of polygons and patterns possible for edge-to-edge regular polygon tilings in the plane is so limited.
It is not surprising that both mathematicians and artists have explored other options. As we will see in the next part of this site, adding additional prototiles introduces an enormous number of new and beautiful tiling possibilities.
With a small change to the rules, it turns out that the forbidden tilings are not forbidden after all ...
