The four vertex types shown below can be extended to periodic tilings of the plane, but only by including additional vertex types. They are, by Kepler's definition, "imperfect congruences".
Johannes Kepler, Harmonices Mundi, Book II, Section 4
As expected, Kepler's definition of imperfect congruence is the reverse of a perfect congruence: in an imperfect congruence the tiling "cannot be continued indefinitely or can be so continued only by introducing meeting points of different kinds". In modern language this would be "introducing vertices of different types".
Roses
Kepler then goes on to distinguish two different kinds of imperfect congruence. In the first kind, the largest figure can be "surrounded by similar meeting points". In the second, which is said to be of "lower degree", the "larger figure cannot be surrounded in such a way that similar meeting points are formed at all its angles".
In many tilings it can be seen that the largest prototile polygon is always or sometimes surrounded by a ring of smaller polygons that intersect with the same vertex type at every vertex of the largest polygon. Kepler does not seem to give a name to this structure - I will call it a rose as it reminds me of a central flower surrounded by petals.
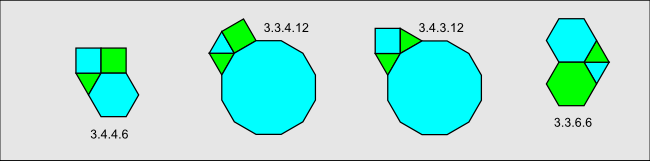
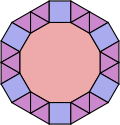
For example, the four vertex types described in this section cannot be extended to a uniform tiling (as I will prove below), but each dodecagon in the first tiling illustrated below (containing the 3.3.4.12 vertex type) is the centre of a rose with alternating triangle and square petals. Each vertex of the dodecagon has the same 3.3.4.12 vertex type even though the tiling as a whole is not uniform. Similar roses occur in some (but not all) tilings containing the other three vertex types (3.3.6.6, 3.4.3.12, and 3.4.4.6).
In fact only the 3.10.15 vertex type does not ever allow the construction of a polygon patch containing a rose and is therefore "imperfect of lower degree". Kepler gives a detailed proof for the case of 3.10.15 (essentially, a rose is impossible because 15 is an odd number).
It is a bit curious that Kepler added a distinction that only applies to one vertex type. This may be a sign that Kepler occasionally uses the term "congruence" to refer to larger patches of polygons in addition to vertex figures. It is indeed true that some tilings of the plane do not contain roses around all the largest polygons.

Kepler's errors
Kepler made two errors in Harmonices Mundi when discussing the vertex types in this family. First, as pointed out by Darrah Chavey, his illustration Kk for the rose associated with 3.4.4.6 is missing three lines and so does not include the central hexagon. He does correctly conclude that the rose "cannot be continued without additional figures" and thus 3.4.4.6 is an imperfect congruence.
Second, when discussing the 3.3.6.6 (Kepler's diagram P) and 3.6.3.6 (Kepler's diagram R) vertex types he fails to state whether these types are perfect or imperfect congruences. In fact 3.3.6.6 is imperfect and 3.6.3.6 is perfect.
Example tilings
As in previous sections, the second column gives a translational unit for the tiling and the third column a skeleton tiling. Each of the tilings contains two vertex types, the first of which is one of the four vertex types covered in this section. There is nothing special about the tilings I have displayed beyond the fact that they prove that these four vertex figures can be extended to a periodic tiling of the plane - I could easily have chosen others.
Interestingly, the 3.3.6.6; 3.6.3.6 tiling shown below has the same translational unit as the 3.6.3.6 tiling shown in the previous section on semiregular tilings, but has a different skeleton tiling.
List of tilings that contain imperfect congruences
3.3.4.12 ; 3.3.3.3.3.3
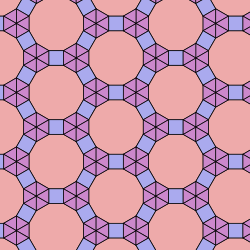
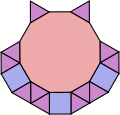

3.3.6.6 ; 3.6.3.6



3.4.3.12 ; 3.12.12

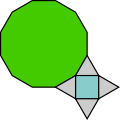

3.4.4.6 ; 3.6.3.6

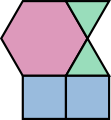

Proving nonuniformity
It is very easy to prove that these four vertex types cannot be extended to uniform tilings of the plane and so are imperfect congruences. We can do this by assuming that such an extension is possible and then deriving a contradiction. The argument is essentially identical in each case, so it can be summarised by adding to the original images of the vertex figures.

In each case:
- Start with the original vertex figure surrounding the vertex with the white dot.
- Extend the tiling assuming the same vertex type by adding the additional purple polygons around the vertex with the green dot.
- This creates a polygon configuration around the red dot that conflicts with the original vertex type.
Thus, in each case, the vertex figure cannot be extended to a tiling without introducing at least one additional vertex type and so the tiling cannot be uniform.
