In addition to the vertex types 3.3.3.3.3.3, 4.4.4.4 and 6.6.6, which Kepler described as the "most" perfect congruences, he identified 8 others as "perfect congruences".[1]
These eight vertex types consist of more than one prototile, but like the "most" perfect congruences, they can be extended to tilings of the plane which have only one vertex type.

The 8 tilings shown below, each extended from one of the above vertex types, are called the semiregular tilings. The 3 regular and 8 semiregular tilings combined form the 11 Archimedean or uniform tilings, so called because every vertex has the same type.
The tilings shown on this page are taken from Wikipedia (as shown in the article List of uniform tilings). As described in the section on regular tilings, I have added translational units in the second column and the skeleton tiling in the third column.
Perfect congruences
List of semiregular tilings
3.3.3.3.6

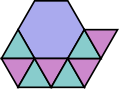

3.3.3.4.4



3.3.4.3.4

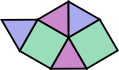

3.4.6.4

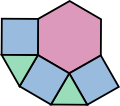

3.6.3.6

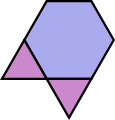

3.12.12

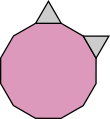

4.6.12
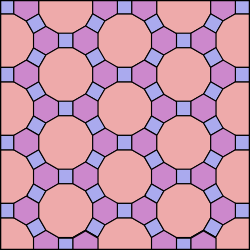
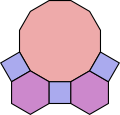

4.8.8



