SI(5) consists of the pentagon, decagon, 5-rhomb and 10-rhomb. According to my calculations, there are 121 distinct ways to combine these polygons to form vertex figures. Here are the seven of them that contain at least one pentagon and decagon:
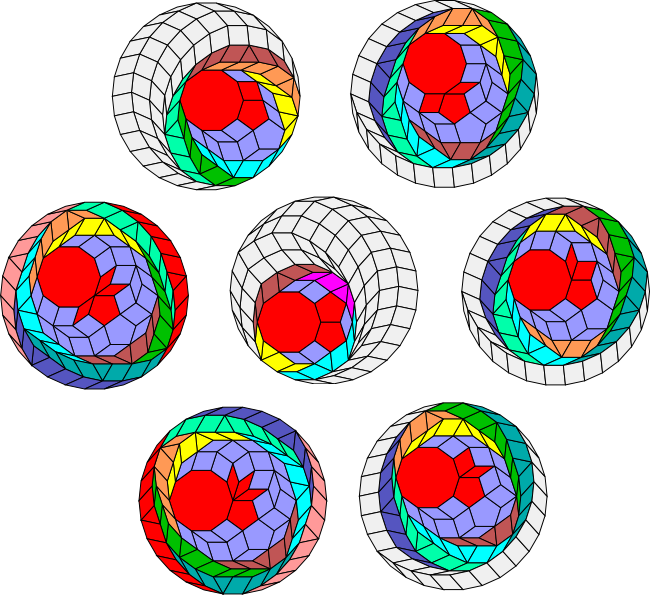
As expected they can be unflattened with a triangle and extended to regular polygons with 2*5*3 = 30 sides. The coloured bits show the zonagons created by unflattening.
All except the central figure consists of a single pentagon and so the pentagon must be mirrorified as described in the extension algorithm before the triangle can unflatten the figures.
Just for fun, I have created a 1280x1024 mosaic that shows all 121 SI(5) vertex figures extended to a periodic tiling, using a simpler colour scheme (the vertex figures are in red). To me, the vertex figures resemble the strange microscopic creatures you can sometimes see in a drop of pond water, each floating in its blue zonagon bubble. This mosaic is crying out for a larger version and I am thinking about possibly turning it into a poster.
