For any n, the rhombic star constructed from twelve 3n rhombic triangles, as described here, is always the same. Thus, any variations in the tilings generated by the universal tiler depend upon the decomposition of the 6n-gon.
Let's consider the hendecagon tilings when n = 11.
We know from the decomposition theorem that if we select the appropriate position function we can decompose the 66-gon into 2, 4 and 6 hendecagons:
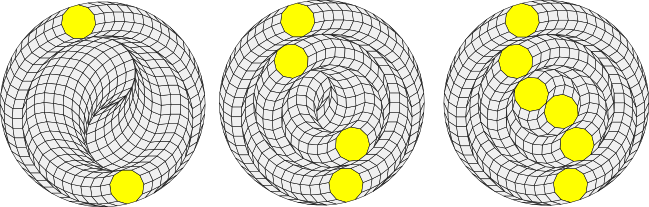
There are more than these possibilities, however. After the first ring of two hendecagons is decomposed, the residual polygon is a 44-sided polygon with edge angles that alternate between π/33 and 2π/33 radians. Because it is irregular, it doesn't have the full 44-fold rotational symmetry of a regular 44-gon, but it does have 22-fold symmetry. Thus, there are many different ways to rotate the residual polygon after it is decomposed. (This is also true of the 55-sided irregular residual polygon that results after the 66-gon is partially decomposed into one hendecagon. It has 11-fold rotational symmetry.)
After the 66-gon is decomposed into two rings of four hendecagons, the residual polygon is a regular 22-gon. Moreover, with the correct choice of position function, it is possible to create a residual polygon that is a regular 33-gon after the 66-gon has been decomposed into three hendecagons. Of course both the 22-gon and 33-gon can be rotated after they are further decomposed or they can be left as is to decompose the 66-gon into more than one type of smaller regular polygon.
Here are illustrations showing the irregular 44-gon, the regular 22-gon and 33-gon, and an alternative decomposition in which the six hendecagons have been rotated into different positions:
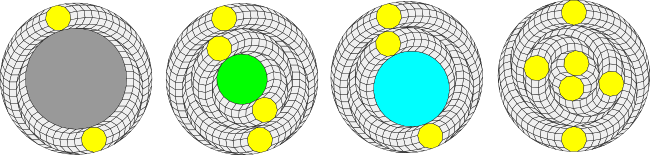
The existence of a decomposition into regular polygons of multiple orders depends as usual on the divisors. 22 and 33 both divide into 66 and so decompositions involving regular 22-gons and 33-gons exist. 44 and 55 do not divide into 66 and so any residual 44 or 55 sided polygons are irregular.
In addition to rotating the residual polygons, it is of course possible to freely rotate any 66-gon in the plane tiling. Since it is possible to replace any 6n-gon in the tiling with any one of these variations, this shows that there are an infinite (indeed uncountable) number of possible periodic tilings of the plane including rhombs and hendecagons (or for that matter any regular polygon).
Having said that, all of the tilings generated using the universal tiler described on this site have the same basic structure with a 6 pointed rhombic star and a 6n-gon (possibly decomposed into smaller regular polygons).
Are there universal regular polygon tilers that produce tilings with a different structure?
That's an interesting question for future research!
In the next sections we'll revisit vertex figures and show how the results described in this section allow us to derive some new conclusions about how certain vertex figures with three polygons can be extended to periodic tilings of the plane.
