
This section provides some mathematical background for the regular polygon tiler described in the previous section.
Fans
Given an integer m >2, take the rhomb with angle π/m. Then add two rhombs with angle 2π/m, three rhombs with angle 3π/m and so on until you have added m-1 rhombs with angle (m-1)π/m.
This structure fans out from the initial π/m rhomb so I call it a fan. There are many possible variations on this basic pattern depending upon the rhombs added at each stage.
Rhombic triangles
One important variation works only for fans of order m = 3n. In this case we start with the rhomb with small angle π/m but stop a third of the way through the process, when we reach the n rhombs of angle nπ/m. Since m = 3n, these rhombs always have the angle nπ/3n = π/3.
This rhomb has the special property that it consists of two triangles joined together. Put another way. the equilateral triangle is half of the rhomb with small angle π/3.
Now split the π/3 rhombs into two triangles and then drop the second triangle from each pair. This creates a tile patch of rhombs and triangles that I call a rhombic triangle. Rhombic triangles act in some ways like equilateral triangles and have many interesting tiling properties. In particular, they can be used to build a universal tiler for regular polygons.
The image below illustrates the rhombic triangle construction process for order 12 = 3*4.
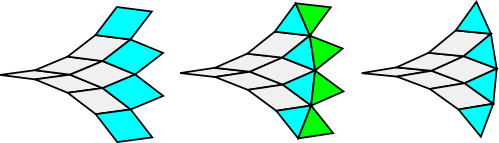
Other rhombic structures
6 rhombic triangles form a rhombic hexagon and adding 6 more triangles to the sides of this rhombic hexagon creates a six-pointed rhombic star.

A 6n tiler
The rhombic star has a very interesting property indeed: a rhombic star constructed from rhombic triangles of order m = 3n tiles the plane with a regular polygon of order 6n!
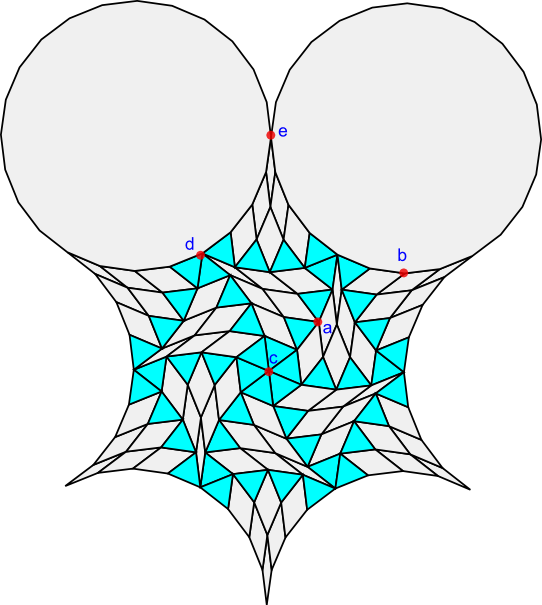
As a specific example, here is the translational unit for a plane tiling with a rhombic star constructed from rhombic triangles of order 12 = 3*4 and two regular polygons of order 24 = 6*4:
Tiling proof
It is worth putting some effort into understanding why a 3n rhombic star tiles the plane with a 6n regular polygon.
In order to show that this construction forms a plane tiling, we must prove that the sum of the angles at each vertex is 2π.
There are only 5 cases to consider. Examples of each case are labeled in the translational unit above.
Edges
Let's start by looking at the rhombic triangle vertices that are not the three tips. There are only two cases here.
Each rhombic triangle has two concave (bends inward) edges and one convex (bends outward) edge.
Let's start with the concave edges. Each vertex is the intersection of two polygons. The two small angles of these polygons are iπ/3n and ( i+1)π/3n for some integer i. However, the second polygon intersects with the large angle of the first polygon.
The large angle of the first polygon is π - (iπ/3n). Thus the sum of the two angles is
π - (iπ/3n) + (i+1)π/3n = π +π/3n = (3n+1)π/3n
Notice that the angles do not depend upon i - they are always the same.
For the convex edge, each angle is the sum of two triangles and the rhomb with small angle (n-1)π/3n.
This is
2π/3 + (n-1)π/3n = (3n-1)π/3n
In case a in the illustration above, a convex edge and a concave edge are placed together.
The sum is:
(3n+1)π/3n + (3n-1)π/3n = 6nπ/3n = 2π
In case b in the illustration above, the concave edge combines with the polygon with 6n sides.
This polygon has interior angles (6n-2)π/6n = (3n-1)π/3n at each vertex. This is the same as the angles at the vertices of the convex edge, and as before the sum of the angles is 2π at each vertex.
Tips
Now we only need consider the three cases for the angles at the tips of the rhombic triangles.
In case c six tips with triangles all intersect in the centre of the rhombic hexagon. The angle is 6(π/3) = 2π.
In case d, four rhombic triangles intersect with a vertex on the edge of the 6n polygon.
Three of the rhombic triangle tips are triangles, and so these sum to 3(π/3) = π. The last tip has angle π/3n. From above, we know that a vertex on the edge of the 6n polygon has angle (6n-2)π/6n. Adding the last rhombic triangle tip to this gives us:
(6n-2)π/6n + π/3n = ((6n-2)π+2π)/6n = 6nπ/6n = π.
Thus the total angle for case d is 2π.
In the final case at e, we have two 6n polygons intersecting with two narrow rhombic triangle tips with angle π/3n.
The sum here is:
2*(6n-2)π/6n + 2*π/3n = (2*(6n-2)π+4π)/6n = 12nπ/6n = 2π
Thus each of the 5 vertex cases has angle 2π and the translational unit tiles the plane.
Beyond 6n
In the next section we will look at how the 6n regular polygon can be decomposed into smaller regular polygons.
