In the previous section I described the KSK algorithm to decompose certain polygons into rhombs.
This algorithm can be extended to a more general algorithm to decompose a large regular polygon into copies of a smaller regular polygon and rhombs.
I worked out the details for this more general algorithm myself and it does not appear to have been published before.
I'll first look at the algorithm for the case when the large polygon being decomposed has an even number of sides. Then at the end of this section I'll look at the case when the large polygon has an odd number of sides.
Position function
The algorithm requires a position function, which is something like the matching function in the KSK algorithm. The position function is given a small and a large regular polygon and it returns an edge on the larger polygon. The smaller polygon is then attached to this edge. The position of the smaller polygon determines a number of associated worms.
The position function has a number of interesting properties. We'll look at those in a separate section.
Small polygon with an even number of sides
We'll start by assuming that the smaller regular polygon also has an even number of sides.
As a specific example, let's again look at the 30-gon and decompose it into hexagons.

As the illustration shows, at each stage we have one hexagon and five worms. I have coloured the a and b parallel edges for each of the worms. The worms are constructed using the same method described for the KSK algorithm. The residual polygon is a zonagon with 30 - 6 = 24 sides.
Since the residual polygon is a zonagon, we could use the KSK algorithm to decompose it into rhombs and then stop with a single hexagon. We can also reapply the more general algorithm to add another hexagon to the decomposition. It turns out that we can decompose the 30-gon into 0, 1, 2, 3, 4 or 5 hexagons.
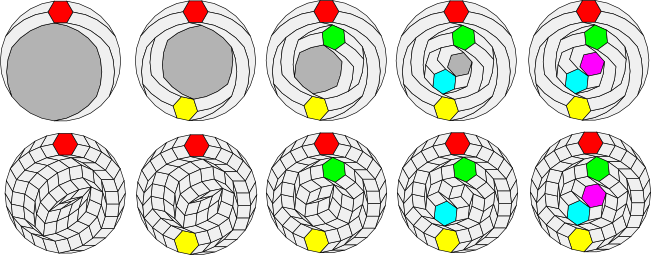
At the penultimate (next to last) stage, notice that the residual polygon is a hexagon! This hexagon can either be dissolved into three rhombs to create a decomposition of the 30-gon with 4 hexagons or maintained as-is to create a decomposition with 5 hexagons. Thus there are no worms involved in the last stage (or you might say that the five worms in the last stage have zero length).
The number of worms created at each stage depends upon the size of the small regular polygon. With a hexagon, it is 5 worms. With a decagon, it is 9 worms.
In the original KSK algorithm, each stage involves splitting the polygon being decomposed into a worm and a residual polygon with two fewer edges than the original polygon.
In this more general case, if the smaller polygon has 2m sides, then each stage involves splitting the larger polygon into one smaller polygon with 2m sides, 2m-1 worms and a residual polygon with 2m fewer edges than the original polygon.
Small polygon with an odd number of sides
What happens if the small polygon has an odd number of sides?
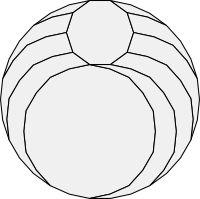
Here's an example for a pentagon:
In general, if the small polygon has 2m+1 sides, then the algorithm splits off 2m worms at each stage.
But in this case, the residual polygon is not a zonagon: it has an odd number of sides!
Fortunately, with the correct position function, we can find the appropriate edge to attach the next odd-sided polygon and its associated worms so that the residual polygon again becomes a zonagon:
Thus if we are decomposing a large polygon with an even number of sides into smaller polygons with an odd number of sides, the smaller polygons naturally occur in pairs.
Since the residual polygon is now a zonagon, we could use the KSK algorithm to decompose it into rhombs and then stop with a single pair of pentagons. We can also reapply the more general algorithm to add more pairs of pentagons to the decomposition.It turns out that we can decompose the 30-gon into 0, 2, 4 or 6 pentagons.
With 6 pentagons the last two pentagons touch one another and there is no residual zonagon left to decompose. We can dissolve the worms into rhombs to get the final result.
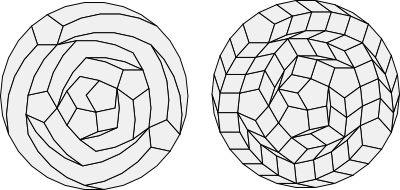
Large polygon with an odd number of sides
It seems futile at first to consider applying our decomposition algorithm to polygons with an odd number of sides. These are not zonagons. In fact, like all odd-sided regular polygons, there is not a single pair of parallel edges. Each edge has a different slope.
If we do persist and apply the algorithm using a small polygon with an odd number of sides, we get an interesting result after the first stage. The residual polygon has an even number of sides, but each of these sides still has a different slope! This is not a zonagon either.
Nevertheless if we continue applying the algorithm we get an amazing result.
Let's look at the specific example of the 25-gon and split off a pentagon at each stage:

After four stages, the residual polygon is a pentagon! Thus the algorithm succeeds after all and decomposes the 25-gon into rhombs and five pentagons. It turns out that the 25-gon can be decomposed into exactly 5 pentagons using this algorithm. Unlike the even sided case, the algorithm cannot generate decompositions with a fewer number of small regular polygons.

In the next section we'll look at some of the basic mathematics behind the decomposition algorithm and we'll see how to generate position functions that place the smaller polygons properly so that these decompositions become possible.
Source code
The source code for the universal tiler and polygon decomposition algorithm is available online and is described in this appendix.
