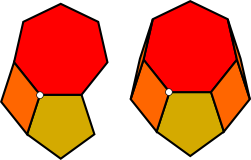
The first step of the solution is to "convexify" the vertex figure by adding additional rhombs to form an irregular convex polygon as shown on the right.
Given the triangle extension theorem described on the previous page, a natural generalisation would be the following:
Definitions
Let the Standard Rhombic Inventory SRI(n) be the set of rhombs with angles:
π/n, 2π/n, ..., (n-1)π/n
Let R be the set of all rhombs and regular polygons.
Two regular polygon extension conjecture
If a vertex figure consists of three polygons from R, two of which are m and n-sided regular polygons, then the figure can be extended to a periodic tiling of the plane using the prototile set consisting of the polygons in the vertex figure and the SRI(mn) set of rhombs.
I'm not sure that this conjecture as stated is true, but I think that I can see a way to prove it if the allowed rhomb set is expanded to SRI(3mn).
Let's consider the vertex figure in the illustration at the upper right. If we can show that this vertex figure can be extended to a 2mn sided regular polygon, then we are done because a 6mn sided regular polygon can be decomposed into three 2mn sided regular polygons and like any regular polygon with a multiple of 6 sides, a 6mn sided regular polygon tiles the plane along with a 3mn order rhombic star.
The first step is to "convexify" the vertex figure by adding additional rhombs to extend the vertex figure to an irregular convex polygon as shown in the illustration.
We can then extend this irregular convex polygon to a regular polygon by essentially running the decomposition algorithm described earlier in reverse.
To see how this works, remember that a 70-gon can be decomposed into two 35-gons and that the 35-gons can in turn be decomposed into either five heptagons or seven pentagons. As is typical for these decompositions, the smaller regular polygons all have different "colours" - they cannot be translated onto each other without rotation.
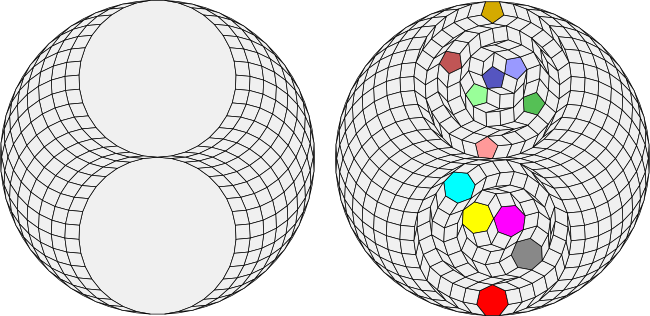
Is it possible to decompose the 70-gon using the same five heptagons and seven pentagons in a different way so that a pentagon and a heptagon are adjacent and form a vertex figure with only a single rhomb?
Yes!
Essentially the extension ("reverse decomposition") algorithm wraps the initial irregular convex polygon with layers. Each layer consists of a single regular polygon and associated worms that extend from its sides. There is one layer for each of the colours missing from the initial vertex figure. The following illustration shows how this works. I have given the regular polygons and their associated worms the same colours as in the previous decomposition of the 70-gon shown above.
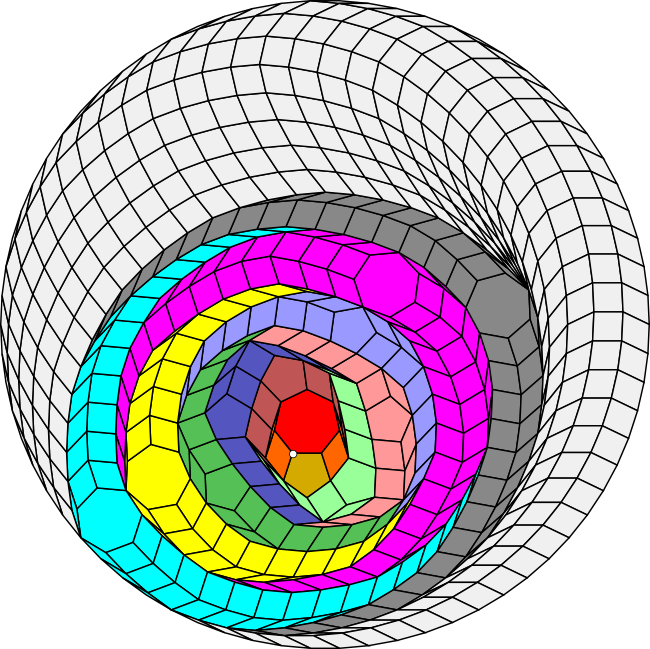
Curiously, the coloured layers do not recreate the entire 70-gon. Instead they create an elliptically shaped zonagon, which can then be extended to the full 70-gon using rhombs alone.
Now that we have extended the figure to a 70-gon, we can then embed three copies of this 70-gon in a 210-gon. Since a 210-gon has a number of sides that is a multiple of 6, it can tile the plane along with the appropriate rhombic star.
Thus, the initial vertex figure can be extended to a periodic tiling of the plane.
I am still working on the Python script for the extension algorithm that generates these images. I'm also investigating whether the same approach might work for three regular polygons or even vertex figures that contain more than one rhomb.
