
At the end of Part 1 of this site, I showed that any vertex figure of regular polygons that can be extended to a periodic tiling of the plane using regular polygon prototiles must contain triangles, squares, hexagons, octagons or dodecagons. In Part 2 of this site, I showed that all vertex figures of regular polygons can be extended to periodic tilings of the plane if we allow rhombs in the prototile sets.
In this section, I have outlined a possible proof that rational rhombs and regular polygons are a complete set, in the sense that any vertex figure of rational rhombs and regular polygons can be extended to a periodic tiling of the plane using only rational rhomb and regular polygon prototiles. No additional prototiles are needed.
In particular, I have the following conjecture:
Vertex figure extension conjecture
Let SI(m) be the set of rhombs and regular polygons with external angles
π/m, 2π/m, 3π/m, ..., (m-1)π/m
Then any vertex figure constructed from polygons in SI(m) can be extended to a regular polygon of order 2mn using prototiles from SI(mn) where n is any odd number that is relatively prime to m.
Corollary
Define a rational rhomb as a rhomb whose angles are a rational multiple of π.
Let R be the set of regular polygons and rational rhombs.
Then any vertex figure constructed from elements of R can be extended to a periodic tiling of the plane using a finite set of prototiles from R.
The set SI(m) is meant to be read "standard inventory of order m" and is inspired by Allan Schoen's concept of a standard rhombic inventory. SI(m) of course also includes regular polygons.
If we think of SI(m) as the pieces of a puzzle, it is worth noting that any SI(m) can be used as the prototile set for a tiling. One method to do this is to simply randomly select and attach together two elements of SI(m), convexify the resulting polygon using the method described below, add another random element to an edge of the resulting convex polygon, convexify it, and so repeat.
This always results in a nonperiodic tiling. Here are examples for SI(5). In the second example on the right, I have randomly chosen only regular polygons at each stage.
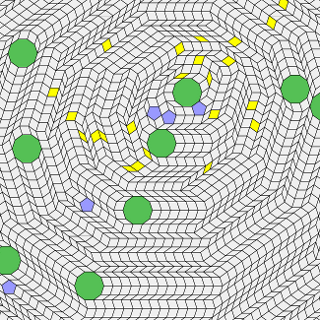

The coloured polygons are the ones added randomly. The others were added through convexification. The same sort of random pattern can easily be generated by starting with a full vertex figure rather than just one or two polygons.
The vertex figure extension conjecture is about the more interesting case of extending a figure to a periodic tiling. In most cases it appears that extending an SI(m) vertex figure to a periodic tiling cannot be done within SI(m) itself and that more "puzzle pieces" need to be added.
I have called this a conjecture because I do not yet have a complete proof. What I do have is an algorithm which appears to have certain remarkable properties as described below. If we can prove these properties, then we can prove that the algorithm can be used to extend any vertex figure to a periodic tiling of the plane and hence prove the conjecture itself.
Here is an illustration of the stages of the algorithm:

Once we have extended a vertex figure to a regular polygon, we are done because as I've shown earlier in the site (although not yet rigorously), any regular polygon can be extended to a periodic tiling of the plane.
The vertex figure extension algorithm
The algorithm has five stages. In my description of these stages below, I make a series of (so far unproven) claims. If and when these claims all have proofs, it would establish that the algorithm works for all vertex figures and so establish the conjecture and corollary stated above.
Stage 1: mirrorify
Take the regular polygons with an odd number of sides. For each polygon type (eg. pentagons), pair the polygon with another polygon of the same type that is rotated by π radians. For every such polygon that cannot be so paired, add a polygon of the same type to the edge opposite the vertex in the vertex figure.
Here are some examples:

In the first example we are adding the mirror image of the triangle and the pentagon to the polygon. There is no need to mirrorify regular polygons with an even number of sides because as pointed out earlier on this site, these polygons are their own mirror images.
In the second example, the top two pentagons form an opposite pair, so we need to only mirrorify the third pentagon.
Claim 1
If we consider a mirrorfied vertex figure as a single (usually irregular and concave) polygon, then this polygon has an even number of sides. Each side has at least one other parallel side.
Stage 2: convexify
Start with a mirrorfied vertex figure of regular polygons and/or rational rhombs selected from SI(m). (Note that any vertex figure of regular polygons and/or rational rhombs is made of of polygons from SI(m) for sufficiently large m.) Make a list of all external vertices with gaps that are less than π. Attach rhombs with angles equal to the gap to each vertex. Repeat until the result is a convex polygon.

In this example, I start with a mirrorified vertex figure constructed from the triangle, pentagon, hexagon and three rhombs with small angle 2π/15. These polygons are all elements of SI(15).
Claim 2
The convexify process always terminates in a convex polygon when applied to a mirrorified vertex figure of rational rhombs and/or regular polygons. The convexified polygon always has the same number of sides as the original polygon and each side has at least one other parallel side.
Stage 3: unflatten
If the original vertex figure was made up of polygons from SI(m), select an n-sided regular polygon where n is an odd integer relatively prime to m.
Define a flat vertex as a vertex whose gap is exactly π radians.
Find a flat vertex in the mirrorified polygon. Attach an n-sided regular polygon and convexify the result. Repeat until the resulting polygon has no flat vertices.
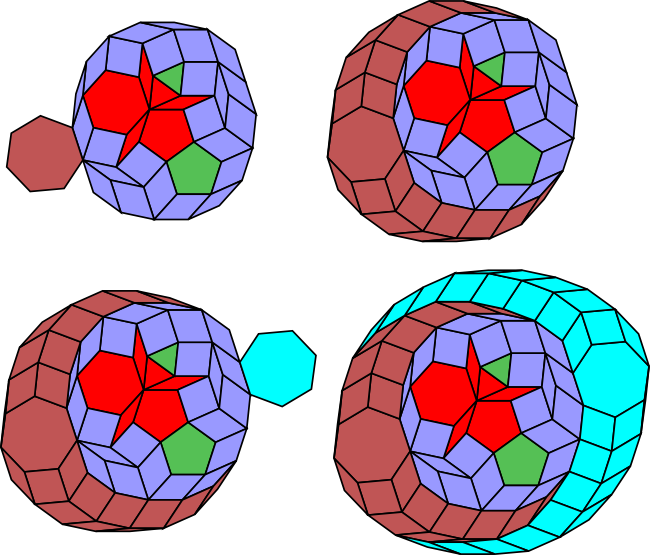
In the above example the unflattening is done by adding heptagons (7-gons) and is completed after two iterations.
Claim 3
Unflattening a mirrorified and convexified vertex figure always terminates in a zonagon.
Stage 4: regularize
Extend the zonagon that results from the unflattening process to a 2mn sided regular polygon.
This can be done as follows:
Find a vertex on the polygon with gap > π + (2π/2mn). Add a rhomb to the vertex to make the gap exactly π + (2π/2mn). Convexify the result and then repeat.
Claim 4
Regularizing a zonagon constructed from elements of SI(mn) results in a 2mn sided regular polygon.
You can see the result of regularization in the first large image above, which shows that the zonagon can be extended to a 210-gon by adding the correct rhombs. This is consistent with the conjecture since 2*15*7 = 210.
Stage 5: extend the regular polygon to a translational unit for a periodic tiling of the plane
Finally, to prove the corollary given above, we must prove this last claim, which has not yet been rigorously proved on the site:
Claim 5
Any regular polygon can be extended to a periodic tiling of the plane using a finite prototile set of regular polygons and rational rhombs.
The algorithm to do this has been explained earlier in this part of the site.
Discussion
For me the most startling of the claims above is Claim 3. It is not clear to me why the algorithm that I have described should always create a zonagon. I make this claim only because in my experiments with a large number of vertex figures the result at this stage is always a zonagon. Probably the best way to find a vertex figure counterexample to my conjecture would be to find one that does not generate a zonagon at this stage.
As we will see in the examples in the next section, regular polygons are needed to unflatten some vertex figures that consist entirely of rhombs. There is a nice balance here. Earlier in the site we discovered that rhombs are needed to extend certain vertex figures of regular polygons to periodic tilings of the plane. Now we see that the reverse is also true - regular polygons are needed to extend certain vertex figures of rhombs to periodic tilings! There seems to be a very close association between regular polygons, rhombs and tilings.
