It is very interesting that, as shown in the last section, any regular polygon with 6n sides can tile the plane using rhombs and triangles.
But we can say much more than this.
If a regular polygon has a composite number of sides, it turns out that there are several (sometimes many) ways to decompose it into smaller regular polygons and rhombs.
Here are some examples for the 30-gon which has 6x5 sides.
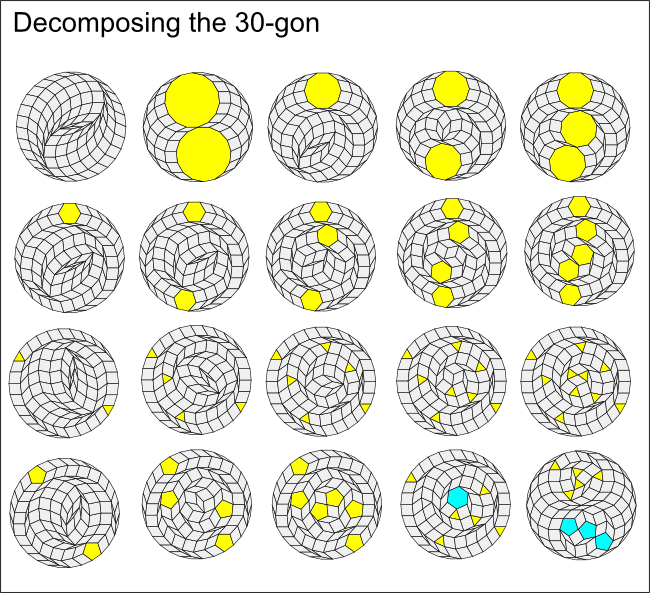
The first row in the illustration shows that the 30-gon can be broken down into all rhombs, two 15-gons or 1,2 or 3 decagons.
The second row shows decomposition into 1, 2, 3, 4 or 5 hexagons.
The third row decompositions in triangles. These always come in pairs, with 2,4,6,8 or 10 triangles.
The fourth row shows decompositions into pentagons. These also come in pairs, with 2, 4, or 6 pentagons. The final two examples show mixed regular polygons: 6 triangles and a hexagon, and 5 triangles and 3 pentagons.
It turns out that the same basic pattern applies to a decomposition of any even-sided regular polygon, and can be described as follows:
Decomposition theorem (even case)
If a regular polygon has j = mn sides where j is even with m > 1 and n > 2, then it can be decomposed into rhombs and:
0,1,2,3,...,m n-sided regular polygons if n is even or
0,2,4,...,m n-sided regular polygons if n is odd.
(Note that this theorem does not cover decompositions into more than one type of regular polygon although the examples above shows that this is often possible. Moreover, this is not a complete list of all the possible decompositions into regular polygons as we will see by the end of Part 3.)
One of the consequences of this theorem is that a 6n regular polygon (n > 2) can always be decomposed into rhombs and 6 n-sided regular polygons, and hence a plane tiling involving 6n-sided regular polygons can easily be converted into one involving n-sided regular polygons. Notice that 30 = 6x5 and one of the examples above shows six pentagons.
In the following sections we'll look more at this result and an algorithm for constructing the above decompositions.
But first, out of curiosity - what happens if the polygon being decomposed has an odd number of sides?
