Decomposition mathematics

After having seen the polygon decomposition algorithm in action, it's time to look at the mathematics of polygon decomposition in more detail to understand why the algorithm works.

Even regular polygon decomposed into odd regular polygons

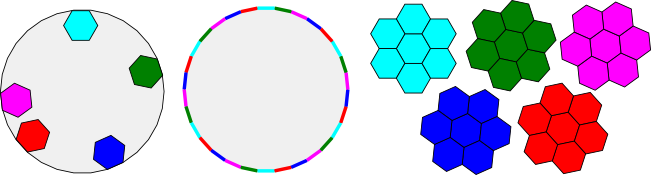
Let's consider the decomposition of the 30-gon into pentagons.

(The above image is linked to a larger version to make it easier to view.)

If we attach a cyan pentagon to the top edge of the 30-gon, we can see that the same pentagon can be attached (using translation but without rotation) to a total of 5 edges of the 30-gon, one for each side of the pentagon. Let's call these the "cyan" edges.

If we choose an edge of the 30-gon that is not one of the cyan edges (call it a red edge), then we can see that there is a red pentagon that can be attached to a total of 5 edges of the 30-gon, one for each side of the red pentagon.

We can do the same thing for dark green, blue, purple, magenta and black pentagons: a total of 6 pentagons altogether.

This enables us to attach colours to each of the 30-gon edges. There are 6 colours, and each occurs 5 times.

It is no coincidence that 6x5 = 30. We can follow the same process for any n-sided regular polygon where n divides 30. In this case, there would be 30/n different colours, each of which would occur n times.

If we choose an n-sided polygon where n does not divide 30, it is easy to see that there would be 30 different colours, each of which would occur only once.

It is the fact that the coloured edges occur multiple times that makes decomposition into rhombs and smaller regular polygons possible.

In the specific case of the pentagons and the 30-gon, the 6 differently coloured pentagons naturally occur in pairs. Each of the cyan edges is parallel to exactly one blue edge (and vice versa). Each of the red edges is parallel to exactly one magenta edge (and vice versa). Each of the dark green edges is parallel to exactly one black edge and vice versa.

Let's attach a blue pentagon to one of the blue edges and use our decomposition algorithm to split the blue pentagon and four worms from the 30-gon:

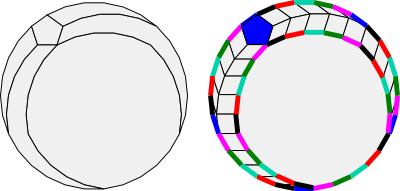
If we render the result into rhombs and show the edge colours of the residual polygon, we can see that the residual polygon has no blue edges. The decomposition algorithm has eliminated them! Notice that rhombs always have edges parallel to the original edges of the 30-gon and so can never introduce new edge colours.

This shows us what the decomposition algorithm is really doing: eliminating edge colours.

If we continue the algorithm for each of the 6 pentagons, we can see that each stage in the algorithm eliminates one edge colour, until we are left with 5 edges of the single magenta edge class, which inevitably surround the magenta pentagon.

(This last image is linked to a larger version to make it easier to see what is going on.)

Choosing a position function

In the previous example, the position function returns the edges in the following order:

This works well for a full decomposition into six pentagons but would not work for fewer pentagons.

To see why, consider what would happen if the 30-gon is decomposed into one, three or five pentagons using this position function. This would create an irregular residual polygon with an odd number of sides. No polygon with an odd number of sides can be decomposed into rhombs.

If we decompose the 30-gon into both the blue and black pentagons, this creates another problem. The residual polygon now has an even number of sides, but these are red, cyan, dark green and magenta edges. As mentioned above, the cyan edges are parallel to the blue edges, and the dark green edges are parallel to the black edges. Since the blue and black edges have been eliminated, the light and dark green edges have no corresponding parallel edges and so the residual polygon cannot be a zonagon and cannot be decomposed into rhombs.

The same problem occurs if four pentagons have been decomposed.

To fix this problem, we can choose a position function that places the pentagons in a different order:

Now each pair of pentagons has parallel edges, so as each pair is eliminated, the remaining pentagons still have matching parallel edges. The residual polygons after the 30-gon is decomposed into two or four pentagons are both zonagons, so this position function allows a decomposition into rhombs and two, four or six pentagons.

This is generally true when decomposing a regular polygon with 2n sides into smaller regular polygons with 2m+1 sides. With the correct position function, the decomposition can include any even number j of (2m+1)-sided polygons, where j ranges from 0, 2, 4, ... to 2n/(2m+1). This is only works if 2m+1 divides 2n of course.

We could also choose a position function that returns the pentagon edges in this order:

The first three pentagons select every second edge going around the 30-gon. As a result, the residual polygon after the 30-gon is decomposed into three pentagons (blue, red and dark green, so half the edges are removed) is a regular polygon with angles twice as large as the 30-gon. In other words, it is a 15-gon. Thus this position function can decompose the 30-gon into rhombs, and either 6 pentagons or 3 pentagons and one 15-gon.

Even regular polygon decomposed into even regular polygons

Let's consider the decomposition of the 30-gon into hexagons.

(The above image is linked to a larger version to make it easier to view.)

This time we find that we can divide the 30-gon edges into 5 colour classes using hexagons. This is very similar to the way we divided the 30-gon edges into 6 colour classes using pentagons.

When we look at parallel edges, however, we see a major difference. The pentagons naturally occurred in pairs, so for example, all the edges of the red pentagon were parallel to those of the maroon pentagon. However, in the even sided case, we see that the edges of each polygon are parallel to edges from the same polygon! In this sense, even sided polygons are their own opposites.

For this reason, no matter how a position function selects edge colours for elimination, the residual polygon at each stage of our decomposition algorithm will always have parallel edges for each edge and thus will be a zonagon. For example, suppose the first stage eliminates cyan. Each set of the remaining green, maroon, blue and red edges will contain its own parallel edges. For this reason, we can stop at each stage and decompose the residual polygon entirely into rhombs. Thus, the 30-gon can be decomposed into 0, 1, 2, 3, 4 or 5 hexagons.

This is generally true when decomposing a regular polygon with 2n sides into smaller regular polygons with 2m sides. Regardless of the position function, the decomposition can include any number j of 2m-sided polygons, where j ranges from 0, 1, 2, 3, ... to n/m. This only works if m divides n of course.

Odd regular polygon decomposed into odd regular polygons

Let's consider the decomposition of the 25-gon into pentagons.

(The above image is linked to a larger version to make it easier to view.)

This time we find that we can divide the 25-gon edges into five colour classes using pentagons. This is very similar to the way we divided the 30-gon edges into colour classes using pentagons or hexagons.

When we look at parallel edges, however, we see a major difference between the other two cases. The five pentagons for the 25-gon have no parallel equivalents at all! In fact the smallest regular polygon that has the full set of parallel colours would be the 50-gon.

For this reason, no residual polygon associated with a decomposition of the 25-gon (or any odd-sided regular polygon) can be a zonagon or decomposed into rhombs. In this case, the only decomposition that works is the one with 5 pentagons (which has the last pentagon as its residual polygon).

This is generally true when decomposing a regular polygon with 2n+1 sides into smaller regular polygons with 2m+1 sides. Regardless of the position function, the decomposition can only be into exactly (2n+1)/(2m+1) regular polygons. This only works if 2m+1 divides 2n+1 of course.

Proof of the decomposition theorem

The decomposition theorem shows that we can decompose the 24-gon into rhombs and 2, 4, 6, or 8 triangles. Other decompositions are possible, however, such as this beautiful decomposition with 24 triangles mentioned in the description of the 3.8.24 Starburst tiling.

The decomposition theorem shows that certain regular polygon decompositions are possible. It doesn't eliminate other options, however, as the example to the right shows. It would be wonderful to provide a decomposition theorem that catalogs all possible decompositions of a regular polygon into rhombs and regular polygons but that will have to wait for now.

The information provided in this section provides most of what is needed for a proof of the decomposition theorem.

I'm still working on a full proof, possibly for publication in a mathematics journal. When and if it is published, I'll provide a link here.

In the next section I'll look into the implications for the universal regular polygon tiler and vertex figures.