In the last section I described an algorithm to extend any vertex figure of rational rhombs and regular polygons to a regular polygon. Since we already know that any regular polygon can be extended to a periodic tiling of the plane, this implies that any of these vertex figures can also be extended to a periodic tiling of the plane.
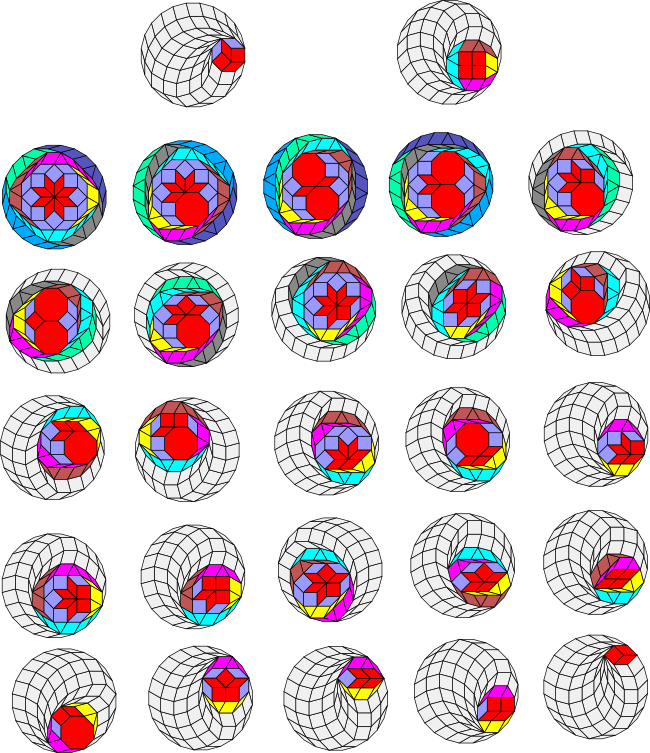
Here are some examples. In the first example, I show all 27 distinct vertex figures constructable from the elements of SI(4). SI(4) has three elements - the square, the octagon and the 8-rhomb (the rhomb with small angle 2π/8 = π/4). The vertex figures are shown in red.
From the vertex figure extension conjecture we would expect that the vertex figures could be unflattened using a triangle and extended to a regular polygon with 2*4*3 = 24 sides and this is indeed the case as can be seen below.
As mentioned in the last section, the polygon created by the unflattening process is always a zonagon. These are shown in colour below, with the colours representing the different stages of convexification and unflattening. (There is no need to mirrorify any of these figures as the square and octagon have an even number of sides.) The light grey rhombs are added by the regularization process at the end.
In the first 6 cases the zonagon is actually a regular polygon. For the first two cases the zonagon is an octagon and a dodecagon respectively. In the next four cases the zonagon is the 24-gon. In all the other cases the zonagon is an irregular polygon.
Although the above examples used the triangle for unflattening the vertex figures, in fact in this case any polygon with an odd number of sides would work. The illustration below shows the vertex figure forming a star of 8-rhombs unflattened using 3, 5, 7, 9 and 11 sided regular polygons, extending the figure to 24, 40, 56, 72 and 88 sided regular polygons respectively. I've changed the colour scheme to highlight the regular polygons.
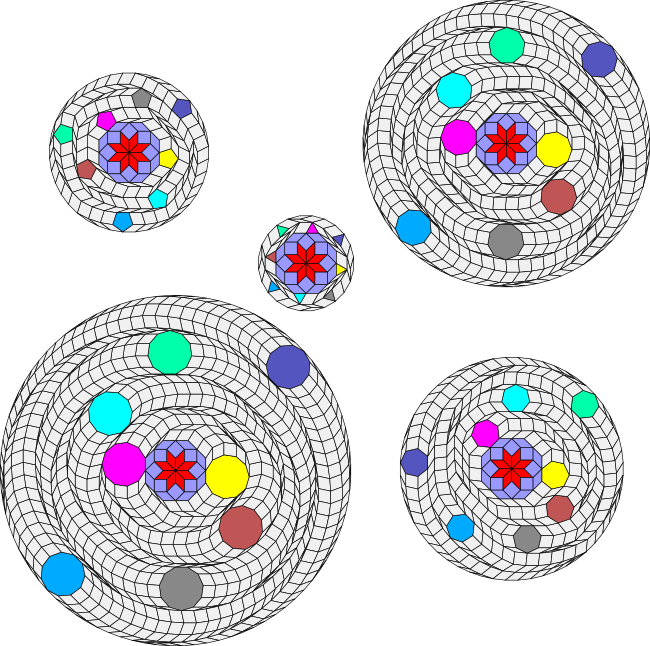
It always takes eight regular polygons to unflatten this specific figure. It is interesting to see that the regular polygons extend out from the central core like spiral arms in a galaxy.
I've described the situation for SI(5), which does require mirrorification, in the next section.
